GAMES202笔记：实时光线追踪

Preface

2018年，Nvidia发布GeForce RTX系列显卡，实现了实时光线追踪(Real-Time Ray-Tracing, RTRT)
RTX中集成了RT-Core模块，用于加速光线追踪中的求交计算（10 Giga rays per second）

虽然目前已经可以做到一秒钟Trace非常多的光线，但是结合分辨率、帧率等因素，并且除去留给其他画面处理工作的时间，实际上RTRT中也只能支持每秒对于每一个像素采样一条光路，也就是1SPP（GAMES202开课于2021年，目前应该能做到更高）

RTRT前置知识

在RTRT中，1 SPP实际包括四条光路：

直接光照
- 从Camera看向Shading Point的光路；
- 从Shading Point看向光源的光路（Shading Point Visibility）；
间接光照
- 从Shading Point采样一个方向，光线沿该方向打到次级光源；
- 次级光源看向光源的光路（次级光源Visibility）

1 SPP path tracing =
1 Rasterization(Primary) +
1 Ray(Primary Visibility) +
1 Ray(Secondary Bounce) +
1 Ray(Secondary Visibility)

其中，第一条光路是从Camera沿着各像素点采样方向Trace光线来找到各个着色点，光栅化也可以完成这个工作且更加快速，因此RTRT每个Sample中的第一条光线的Trace通常直接替换成一次光栅化
RTRT_1SPP

根据GAMES101光线追踪作业的经验，我们知道，1SPP的光追会产生非常非常Noisy的结果
因此，RTRT中最为核心的技术其实并非Ray-Tracing（Ray-Tracing部分基本没有太多新技术，只是有了新硬件加速其过程），而是Denoising
RTRT_Denoising

实现RTRT有如下两个目标：

Quality (No overblur, No artifacts, keep all details…)
Speed (< 2ms to denoise one frame)

由此可见，此前的各类降噪方法都是无法符合要求的

Temporal Denoising in RTRT

RTRT中进行降噪最主要依靠的就是时间性方法（与时间性抗锯齿TAA非常类似）
时间性的降噪基于以下基本思想：

认为之前的帧都是已经降噪完毕的，并且可以复用其中的信息
假设场景的运动是连续的
使用Motion Vector来找到当前帧中的位置对应先前帧中的位置
通过以上复用的方法，本质上就是变相增加了SPP

MotionVector

G-Buffer

Geometry Buffer几何缓冲区存储的是渲染过程中可以免费获取（开销很小）的额外辅助信息。通常，其中可以存储每个像素的深度值、法线、世界坐标等等
G-Buffer记录的是Camera能看到的像素的信息，因此只有屏幕空间的信息
GBuffer

Back Projection

Temporal Denoising中最核心的工作是Back Projection，即在先前帧中找到当前帧中的点的对应点
用一个更为精准的说法就是：假设当前帧为第 $i$ 帧，Back Projection就是要找到，第 $i-1$ 帧中的哪一个像素所包含的位置区域（或者点）与第 $i$ 帧中的像素 $x$ 包含的位置区域（或者点）是一致的
BackProjection

Back Projection执行的步骤如下：

从G-Buffer中取得第 $i$ 帧中像素 $x$ 对应点的世界坐标 $s$
我们知道一个点从世界坐标变换到屏幕坐标经历了MVP变换以及视口变换，于是将像素坐标 $x$ 变换回世界坐标 $s$ 的表达式为： $s=M^{-1}V^{-1}P^{-1}E^{-1}x$ (此处 $x$ 为像素 $x$ 在屏幕空间的二维坐标append上它对应的深度)
假设上一帧对应点的世界坐标为 $s^{\prime}$ ，从上一帧世界坐标变换到当前帧的世界坐标的变换为 $T$ ，则有 $s^{\prime}\,\underrightarrow{T}\,s$ , thus $s^{\prime}=T^{-1}s$ (这里的交换 $T$ 我们可以通过物体、相机在帧间的变换求得)
将世界坐标 $s^{\prime}$ 通过第 $i-1$ 帧的MVP和视口变换，得到第 $i-1$ 帧中对应的屏幕空间坐标： $x^{\prime}=E^{\prime}P^{\prime}V^{\prime}M^{\prime}s^{\prime}$

注：上述过程很像CV领域中的特征点匹配、光流法等等，虽然CV领域已经将这些工作做得非常好了，但是基于深度学习的方法对于RTRT而言大都还不够快速，而且上述Back Projection方法利用的是实际场景的变换求得对应点，这是百分之百准确的

Temporal Accumulation/Denoising

有了Back Projection求得的对应点，就可以对其进行降噪了
首先，对当前帧本身进行一个降噪，然后再利用先前的帧进行时间性降噪（线性blending）：

\begin{aligned} \bar{C}^{(i)}&=Filter[\tilde{C}^{(i)}] \\ \bar{C}^{(i)}&=\alpha\bar{C}^{(i)}+(1-\alpha)C^{(i-1)},\,\alpha=0.1 \sim 0.2 \end{aligned}

其中，上标 $-$ 表示降噪后，上标 $\sim$ 表示未降噪，上一帧 $C^{(i-1)}$ 没有上标是因为通常认为先前帧都是经过降噪处理完毕的。 $\alpha$ 取值 $0.1 \sim 0.2$ 意味着当前帧降噪结果有 $80\%\sim90\%$ 的贡献来源于先前的帧

如下为UE4中进行1spp光线追踪及其降噪后的效果
UE4_1sppRayTracedGI
UE4_1sppRayTracedGIDenoised
UE4_RayTracedGIGroundTruth
注：滤波降噪绝对不应该使得一张图像变亮或变暗。那么为什么我们看降噪前后两张图像明显感觉降噪后更亮呢？其实，两张图像理论上是一样亮的。我们在GAMES101 Path Tracing中知道，光线追踪是无偏的算法，其能量是守恒的。但无偏只是意味着其能量的均值与实际无偏，并不代表其整体分布与实际相同，而使用1spp时，我们Tracing到的能量往往会集中于采样点，导致其上能量巨大，其亮度超过了显示器的最大值，因此被做了0-255的clamp，那部分超出的亮度就因此损失，所以导致画面看起来变暗了

Temporal Failure

时间性的信息并不总是有效的，比如下面这些情况就会导致其失效

Failure Case 1: Switching scenes (Burn-in period)
Failure Case 2: Walking backwards in a hallway (Screen space issue)
Failure Case 3: Suddenly appearing background (Disocclusion, essentially screen space issue)

对于上述情况，如果盲目地使用Temporal Denoising方法则会导致画面物体出现Lagging（拖尾）现象
Lagging

Adjustments to Temporal Failure

目前，解决Temporal Failure问题通常有两种方法——Clamping和Detection
Clamping
Clamping方法是先将上一帧结果的像素值Clamp到与当前帧足够接近的范围内，再进行Blend

Detection
Detection方法是检测时间性的信息是否可以用
比如，可以使用Object ID来判断，在前一帧找到的对应点是否位于和当前帧相同的物体上，如果找到的不是一个物体，则认为该点的时间性信息不准确，而不予使用
利用诸如此类的检测方法，我们可以调整该点Blend时候的 $\alpha$ 值
但是这样也会因为更少使用时间性信息，更多使用当前信息，而重新引入噪声，此时可能需要调整对当前帧的滤波等

More Temporal Failure

Detached/Lagging Shadows
如果场景中物体没有产生任何移动，但是光源在运动，从而使得物体的阴影产生运动。此时，Motion Vector告诉我们物体没有动，Temporal Denoising可以直接找同样的点，于是前后帧不同的阴影就会被blend，而导致阴影产生拖尾现象
TemporalDetachedShadow

Glossy Reflection Lagging
GlossyReflectionLagging
在UE中经常可以看到类似情况，当移动椅子而Glossy材质的地面不动时，Motion Vector告诉我们地面没有移动，因此可以找一样的作为Temporal信息，于是地面上的反射会将当前帧与前一帧blend起来，导致其反射出来的椅子比实际的椅子运动要滞后

Spatial Denoising in RTRT

Implementation of Filtering

图像滤波通常就是（使用低通滤波器）将一张Noisy的图像中的高频噪声滤除。Spatial Filtering则是限定仅在原图像空间内完成滤波
ImplementationOfFiltering

滤波过程就是输入为含噪声图像 $\tilde{C}$ ，以及进行滤波的滤波核 $K$ （cloud vary per pixel），输出去噪后的图像 $\bar{C}$ 的过程

以高斯滤波器为例，对于每个像素 $i$ ，其周围的任何像素 $j$ 都会对其滤波结果有贡献，该贡献大小取决于 $j$ 到 $i$ 的距离（其实就是卷积）
GaussianFilter
高斯滤波器伪代码如下：

For each pixel i
  sum_of_weights = sum_of_weighted_values = 0.0
  For each pixel j around i (including i)
    Calculate the weight w_ij = G(|i - j|, sigma)
    sum_of_weighted_values += w_ij * C^{input}[j]
    sum_of_weights += w_ij
  C^{output}[I] = sum_of_weighted_values / sum_of_weights

注：这种实现的好处在于其对滤波结果进行了归一化，因此不要求滤波核权值总和为1，也能保证滤波后的能量守恒，从而保证滤波后的图像不会变亮或变暗

Bilateral Filtering

使用上述高斯滤波器进行滤波，图像上每个像素的滤波结果都是其周围像素值根据高斯滤波核加权平均的结果，也就是说所有像素都会以同一种方式被模糊掉，包括图像中的物体边缘
注：也可以这样理解，图像中物体的边缘位置像素颜色变化较剧烈，也就说边缘位置是高频信号，而我们的滤波是进行低通滤波，自然会将这些边缘的高频信号滤除，因此会产生模糊
ProblemOfGaussianFiltering

但是人们通常希望滤波去噪的同时保留图像中锐利的边缘，为此引入了双边滤波

双边滤波的基本思想如下：

首先，认为图像中的物体边界是图像中颜色变化剧烈的位置
对于像素 $i$ 的滤波过程中，如果其周围的像素 $j$ 的颜色与其差异过大，（则认为两个像素位于边界两侧）则减少像素 $j$ 对其贡献

双边滤波的滤波核公式如下：（式中表示像素 $(i,j)$ 和 $(k,l)$ ）
BilateralFilteringFormula

双边滤波效果如下，可以看到水面、山体等处的纹理因滤波而模糊，但其边缘依然清晰锐利
BilateralFilteringResult

Cross/Joint Bilateral Filtering

对比上述高斯滤波与双边滤波，可以看到高斯滤波实际上是使用了像素间的距离作为取权值的标准，而双边滤波则是使用了像素间距离以及像素间颜色之差两个标准
如果加入更多特征作为标准来指导滤波，那就有了联合双边滤波

那么这些额外的特征信息从何而来呢？答案就是G-Buffer
JointBilateralFilteringGBuffer

前面我们提到，在1 SPP光线追踪的第一步光栅化过程中我们可以额外记录场景的法线、深度、Object ID、Albedo等其他信息成为G-Buffer，而在后续步骤中G-Buffer中的信息便成为我们可以免费获得（开销很小）的额外信息
注：以Object ID为例，如果像素 $i$ 和像素 $j$ 的Object ID不同，则认为其不在一个物体上，因此应当减小 $j$ 对 $i$ 的贡献。其他信息，如深度、法线方向等也类似。总之就是引入更多的标准来指导滤波操作

使用G-Buffer作为联合双边滤波还有一个极大的好处，就是G-Buffer本身是没有噪声的
注：这里没有噪声意思是G-Buffer是在第一步光栅化中直接得到的真实值。我们知道，由光线追踪渲染出的图像由于SPP的限制会含有很多噪声，在双边滤波过程中，当像素 $i$ 和 $j$ 颜色差距较大时，我们并不知道是颜色确实差距大，还是因为噪声的影响。而G-Buffer不依赖光线多次弹射，自然不受SPP的限制，不会引入噪声

补充说明

滤波核只要能表示权重与虽像素间各种距离（物理距离、颜色距离、深度距离等）衰减即可，并不是一定要用高斯函数
BilateralFilteringNotes1

Implementing Large Filters

联合双边滤波通常对单一标准限制不严格，而其联合起来的滤波效果较好，也就是说单一标准下其滤波核可能会取得比较大

回想一下前面所述的滤波的具体操作，可见当滤波核很大时，滤波操作的计算量非常大，使用 $N\times N$ 卷积核时，对于每个像素就要循环 $N\times N$ 次
对于这个问题，工业界通常有两个解决思路

Sol.1 Separate Passes

Separate Passes方法就是将一个 $N\times N$ 滤波分成一个 $1\times N$ 水平滤波和一个 $N\times 1$ 竖直滤波，于是对于每一个像素的滤波，访问周围像素的次数从 $N^2$ 变为了 $N+N$
SeparatePassesFiltering

这里为什么能拆分成两个Pass呢？
首先，2D高斯函数函数本身就可以拆分成两个1D高斯函数的乘积：

G_{2D}(x,y)=G_{1D}(x)\cdot G_{1D}(y)

而我们又知道，滤波本质上就是做卷积，结合2D高斯函数的拆分，该卷积可以写成：

\iint F(x_0,y_0)G_{2D}(x_0-x,y_0-y)\mathrm{d}x\,\mathrm{d}y = \int\bigg(\int F(x_0,y_0)G_{1D}(x_0-x)\mathrm{d}x\bigg)G_{1D}(y_0-y)\mathrm{d}y

但是，这个方法需要滤波核是可拆分的。双边滤波的滤波核理论上不符合这个条件，但是实际上只要其滤波核不过于大，强行使用Separate Passes方法得到的效果也很不错

Sol.2 Progressively Growing Sizes

该方法的核心就是使用逐次增大的滤波核进行多次滤波
也就是CV领域常用的空洞卷积(A-Trous Convolution)
具体思想如下：

使用多个Pass进行滤波，每个Pass中使用的滤波核都是 $5\times5$ 大小
随着Pass增加，滤波的步长也增加，第 $i(i=0,1,2,...)$ 个Pass的步长为 $2^i$

注：当 $i=4$ 时，本质上就是进行了 $64\times64$ 的滤波，此时原本卷积 $64\times64$ 的计算量减小为 $5^2\times5$
ATrous

那么，为什么这种方法是奏效的呢？
我们需要考虑的主要有两点：为什么逐次增大的滤波核是有效的？为什么逐次增大步长的采样不会出问题？

对于第一个问题，我们可以理解成：更大的滤波核相当于更低通的滤波器
于是逐次增大滤波核相当于从高频信号开始，每次多滤除一点点比上一次更低频的信号（准确地说，每一次低通滤波其的截止频率都是上一次的一半），只是原本一次性滤除的信号在这里分成了多次滤除

而对于第二个问题，我们知道采样在频域上相当于搬移频谱，而根据奈奎斯特采样定理，当采样频率小于两倍的信号最高频率就会出现频谱混叠导致失真。
我们逐次增大采样步长相当于每次减小频谱搬移的距离，按理来说应该越来越会出现混叠，但是别忘记我们每一个Pass中逐次滤除了更为低频的噪声，因此我们每一次搬移的频谱实际上都要比前一次更窄，因而不会产生混叠
更准确地说，每次采样的频率都是上一次的一半，而每一次低通滤波其的截止频率都是上一次的一半，因此频谱宽度是上一次的一半，因此每一次采样都恰好不会发生混叠
ProgressivelyGrowingSizes

Outlier Removal (and Temporal Clamping)

如前所述，在光线追踪中，使用了采样的方法，因此会出现某些像素Trace后结果值特别大的情况，导致渲染结果出现特别亮的点，这些点就是所谓的Outlier。这些Outlier与降噪滤波中通常认为的图像空间的噪声并不一样，因为图像空间中的噪声最亮也就到图像像素的最大值，但是光线追踪中Path采样的结果可能因为能量集中于该点而导致其亮度非常大，超过像素最大值。在这种情况下进行滤波，很可能导致原本一个很亮的点被晕开，变成一片较亮的区域

因此，必须在滤波之前移除那些Outliers
注：Outlier Removal会使得能量不守恒，从严谨的物理层面来看这个方法并不正确，如果想要正确的结果必须等待更多的采样，但是在RTR中我们等不起，只能向效率妥协了

Outlier Detection and Clamping

Outlier Detection通常取每一个像素周围 $7\times7$ 的区域，计算该区域的均值 $\mu$ 和方差 $\sigma$ ，如果当前像素的值在 $[\mu-k\sigma,\mu+k\sigma]$ （ $k$ 通常取1-3）范围之外，就认为是Outlier

而Outlier Removal/Clamping则是将上述超出范围的Outlier值Clamp到这个范围内

注：这里的Outlier Clamping和前面提到的Temporal Clamping非常类似。Temporal Clamping中对当前帧的像素取其周围一块区域计算均值和方差得到一个范围，判断其对应的前一帧的像素值是否超出范围，如果超出范围则将其Clamp到该范围内

Specific Filtering Approaches for RTRT

Spatiotemporal Variance-Guided Filtering (SVGF)

SVGF与前述基础的Spatio-Temporal降噪的RTRT比较类似，也是分为了Spatial和Temporal两部分进行降噪，不过其在此基础上增加了Variance Analysis和其他小Tricks

SVGF-Joint Bilateral Filtering

在SVGF的Spatial Denoising同样使用了联合双边滤波，其中使用了3个特征信息（深度、法线、）来指导滤波
SVGF_result

Depth

SVGF的联合双边滤波首先使用深度信息作为指导

考虑以下情形，A点和B点在同一个Box的同一个侧面上，按理来说在滤波过程中A点应该比较多地贡献到B点，但是由于该表面侧对着Camera，导致A,B两点深度距离较大，在传统的双边滤波中A点反而会较少贡献到B点，这显然不合理
SVGF_depth

为了解决上述问题，引入如下加算关于深度的滤波权重的公式：

\omega_z=\exp\bigg(- \lvert z(p)-z(q) \rvert \bigg/(\sigma_z\lvert \nabla z(p)\cdot(p-q) \rvert+\epsilon)\bigg)

其宏观上的思想概括来说就是，不直接使用两点的深度之差作为指导，而是使用两点深度在点A的法线方向上的差值作为指导（这就是为什么使用了梯度），这种情况下，A点与B点的实际深度虽然差距较大，但是因为在一个平面上，使用改进后的公式求得的Distance并不大，因此点A依然可以较多地贡献到点B
注1：其具体实现，SVGF原文中说：Nabla z is the gradient of clip-space depth with respect to screen-space coordinates，即 $\nabla z(p)$ 是点p处在裁剪空间(MVP变换后，经透视除法变为NDC前)的深度相对于屏幕空间坐标的梯度，以上图来说，这个梯度的方向应该是在屏幕空间中从B指向右侧。这个其实与闫令琪老师说的法线方向本质上是相同的，因为在屏幕空间中一点深度下降最快的方向通常都是其法线在屏幕空间中的投影方向，只不过在屏幕空间中计算可以降到二维

注2：这个公式乍一看会觉得有点奇怪，其实不能直接将指数的分母部分认为是在法线方向上深度的差值，应当将其指数（除掉负号的部分）作为一个整体理解成优化后的深度差值，否则会得出相反的结论。实际上可以这样理解，这个公式本身是随两点深度差值增大而衰减的函数，而优化后的深度差值是通过引入分母中的部分来抑制那部分本应该贡献更大的点的权重衰减。

Normal

SVGF中的联合双边滤波使用的第二个信息是法线方向的差异，公式如下：

\omega_n=\max(0,n(p)\cdot n(q))^{\sigma_n}

两点法线方向差异越大，相互的贡献越小，其中 $\sigma_n$ 用来控制曲线衰减的快慢（就像GAMES101中Blinn-Phong模型控制高光项衰减那样）
注：如果使用了法线贴图，则上述计算需要使用原始的法线，而不能使用经由法线贴图改变后的法线

Luminance

SVGF的联合双边滤波使用的最后一个信息是Luminance，即使用像素灰度值
其宏观的基本思想是，使用两点间灰度值之差的同时，考察点 $p$ 灰度值的标准差，如果这个标准差过大，则认为很可能取到了噪点，因此不能太相信此时的两点灰度差，因此需要减小权重，这也是SVGF中Variance-Guided的由来

\omega_l=exp\bigg(- \lvert l_i(p)-l_i(q) \rvert \bigg/\big(\sigma_l\sqrt{g_{3\times3}(\mathrm{Var}(l_i(p)))}+\epsilon \big) \bigg)

其中， $\sigma_l$ 控制衰减速度， $\epsilon$ 防止分母为0

注：与SVGF利用深度信息的部分类似，这里也不能简单地用宏观的基本思想来理解上面的公式，否则可能错误地得出相反的结论。对于公式可以这样理解，对于A,B两个灰度差值较大的点，如果点B不是噪点，那么就不应该太相信与其相差太多的点A，但如果点B是噪点呢，它本就应该和点B相差较大不是吗，因此引入上式中的标准差，当点B标准差较大则认为是噪点，此时将其放在分母中起到了抑制权重衰减的作用，让点A更多贡献到点B，真正起到滤除噪声的作用

具体实现上一般分为三部分：

先进行Spatical上的操作，取得一帧内该点附近 $7\times7$ 的空间计算 $\mathrm{Var}$
再利用Temporal信息，使用Motion Vector取得该点在先前帧中对应的点，计算加权平均 $\mathrm{Var}$
当前帧可认为其中各点都完成了前面两步操作，而对于该点取其周围 $3\times3$ 空间的值再做一次加权平均(式中 $g_{3\times3}$ )

SVGF Failure

SVGF也如传统的Spatical-Temporal方法，由于需要使用Motion Vector找到先前帧中对应的点，因此对于场景不动光源移动的情况也同样会出现阴影拖影的现象

Recurrent AutoEncoder (RAE)

RAE是使用神经网络，将RTRT得到的Noisy的结果作为输入，并使用G-Buffer作为指导，进行降噪后的图像。

使用G-Buffer只能达到Spatial Denoising的目的，而RAE使用了循环神经网络(RNN)，简单来说就是网络中每个隐藏层的输出不只流向其下一层，还要回过来重新作为自己的输入，因此利用了Temporal信息，这也是其名称中Recurrent的由来
RNN

而其中的AutoEncoder具体来说是一个U-Net，该网络是一个Encoder-Decoder结构，左半边Encoder逐层进行特征提取，然后与右半边Decoder上采样的特征图进行拼接构成不同层级的特征图
U-Net
U-Net
RAE Architecture
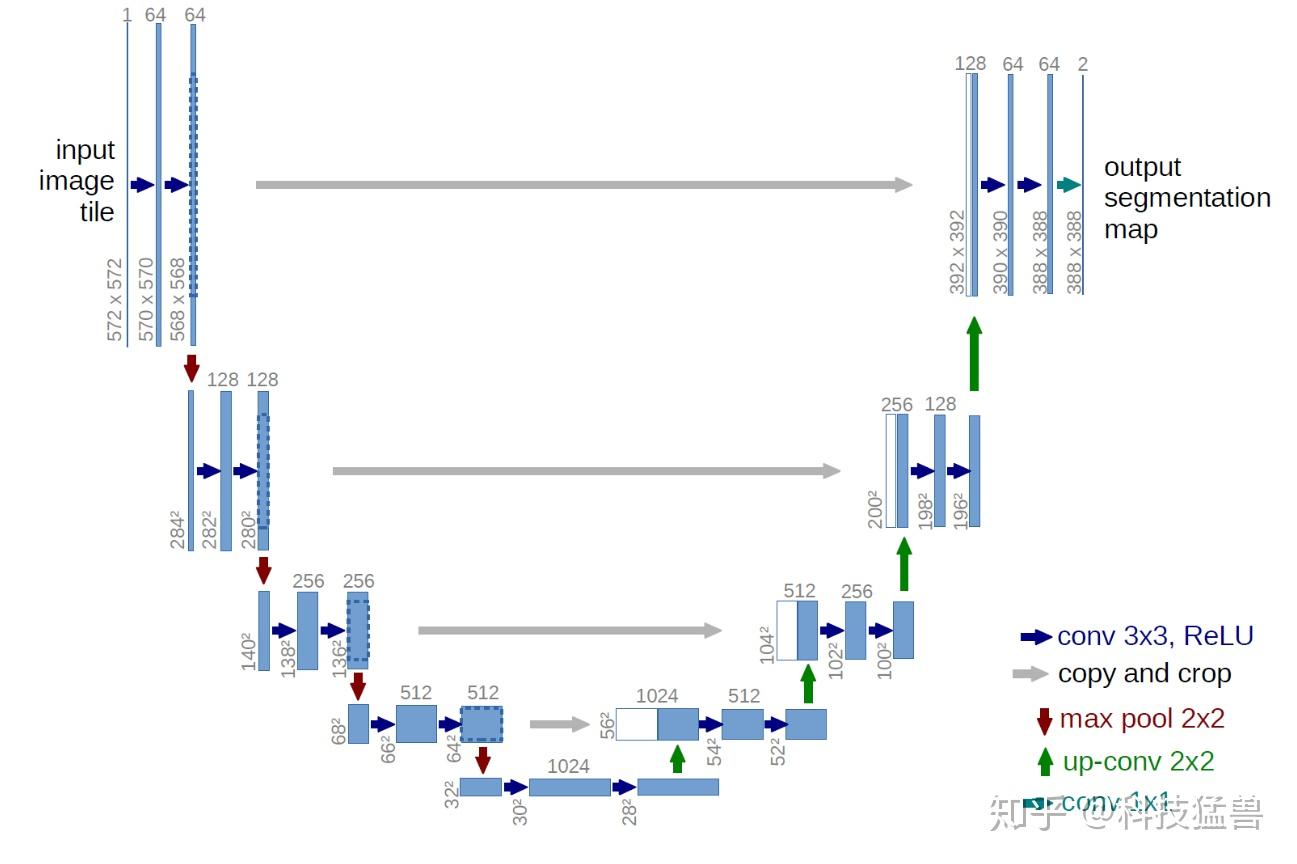
RAE_architecture

RAE由于使用神经网络，因此其速度较慢。同时Ghosting现象也依然时有发生

不过，RAE最主要的优点在于它利用神经网络来学习降噪用的信息，而没有使用Motion Vector，因此对于先前提到的Camera在走廊中后退的情况，就不会因为Motion Vector找不到屏幕周围新进来的点的对应而失效的问题，但是至于神经网络学到了什么，如何利用信息对新进入屏幕的点降噪，我们就不得而知了。

这种基于神经网络的方法虽然速度较慢，但是其速度表现受SPP影响不大，像SVGF这样的方法随着SPP增加计算量显著上升，但是RAE可以保证基本相同的性能表现，同时由于SPP提升，其降噪的效果也随之提高

Nvidia的光线追踪引擎Optix中就有使用一种基于RAE简化的神经网络模型（去掉了其中的循环连接，不使用Temporal信息），在高SPP情况下的结果非常优秀

随着Tensor Core的出现，神经网络在RTR中的应用逐渐成为现实