GAMES101作业8：质点弹簧系统

Segmentation Fault (Core dumped)问题解决记录

我遇到的Segmentation Fault (Core dumped)问题不同于课程BBS上有朋友提出的那种，我不是写了代码后因为代码问题导致出错的，而是直接编译运行作业8的框架就报了这个错误，说明并非代码问题。我始终没有找到与我遇到相同问题的朋友，因此解决这个问题花了我不少时间，因此这篇文章特意保留了我搜索解决这个问题的简单记录，希望能帮助到遇到同样问题的朋友们。

------------------------------------------------------4.6 分界线---------------------------------------------------------
作业8一直出现segmentation fault的问题，即便是直接使用作业框架运行也是如此，问题可能不是出在作业的代码上。

我使用gdb查看过生成的core文件，如下
gdbcore
于是在工作区搜索createKeyTable()函数

问题似乎出在了glfw库中？真见鬼了…

感觉也不像是glfw的问题。我下载了其他朋友完成的作业8在我电脑上运行，仍然是segmentation fault.

研究这问题一整天了，暂时实在没法解决，目前我的猜测是我这台电脑ubuntu有点问题，后续有空继续尝试解决，或者等七月回家之后换台设备再次尝试。
作业8只能暂时搁置了，等后续问题解决之后再补上这篇文章以及github仓库。

------------------------------------------------------4.7 分界线---------------------------------------------------------

想不到第二天居然解决了
我找到了这篇文章——Resolving Segmentation Fault (“Core dumped”) in Ubuntu.文章中给出了解决Ubuntu系统下Segmentation Fault (Core dumped)问题的方法，我先使用了第一种命令行方法，结果没想到把系统搞崩了，Ubuntu桌面没了，重新装了一下桌面进去试了一下代码，没能成功解决。然后我尝试了一下第二种方法，开机进入Advanced options for Ubuntu，选择Run Ubuntu in the recovery mode，然后Repair broken packages，修复完毕后进入系统运行代码发现居然成功了。
repaired

如果你也遇到了直接编译运行作业8代码框架也会出现Segmentation Fault (Core dumped)的问题，或许也是因为Ubuntu系统的问题，不妨试一下这个方法。
注：完成作业过程中，我某次开机重启后，发现再次出现Segmentation Fault (Core dumped)问题，不过重新使用一次上述的第二种方法后又成功解决了。

作业描述

本次作业将实现弹簧质点系统

主要工作如下：

Rope::Rope in rope.cpp: 完成Rope类的构造函数，实现连接绳子的约束；
Rope::simulateEuler in rope.cpp: 利用欧拉方法实现胡克定律；
Rope::simulateVerlet in rope.cpp: 实现显式Verlet方法；
Rope::simulateVerlet in rope.cpp: 向显式Verlet方法积分的胡克定律中加入阻尼。

完成作业

Rope::Rope

// in rope.cpp
Rope::Rope(Vector2D start, Vector2D end, int num_nodes, float node_mass, float k, vector<int> pinned_nodes)
{
    // TODO (Part 1): Create a rope starting at `start`, ending at `end`, and containing `num_nodes` nodes.

    // Comment-in this part when you implement the constructor
    // for (auto &i : pinned_nodes) {
    //     masses[i]->pinned = true;
    // }
    Vector2D step = (end - start) / (num_nodes - 1);
    for(int i = 0; i < num_nodes; ++i){
        masses.push_back(new Mass(start + step * i, node_mass, false));
        if(i > 0){
            springs.push_back(new Spring(masses[i-1], masses[i], k));
        }
    }
    for(auto &i : pinned_nodes){
        masses[i]->pinned = true;
    }
}

根据传入的起始与终止位置以及质点数量构造质点，step为质点间的间距，在相邻两质点间构造弹簧，弹簧系数为k.最后的for循环根据传入的pinned_nodes将对应质点设为固定的。

编译运行
rope

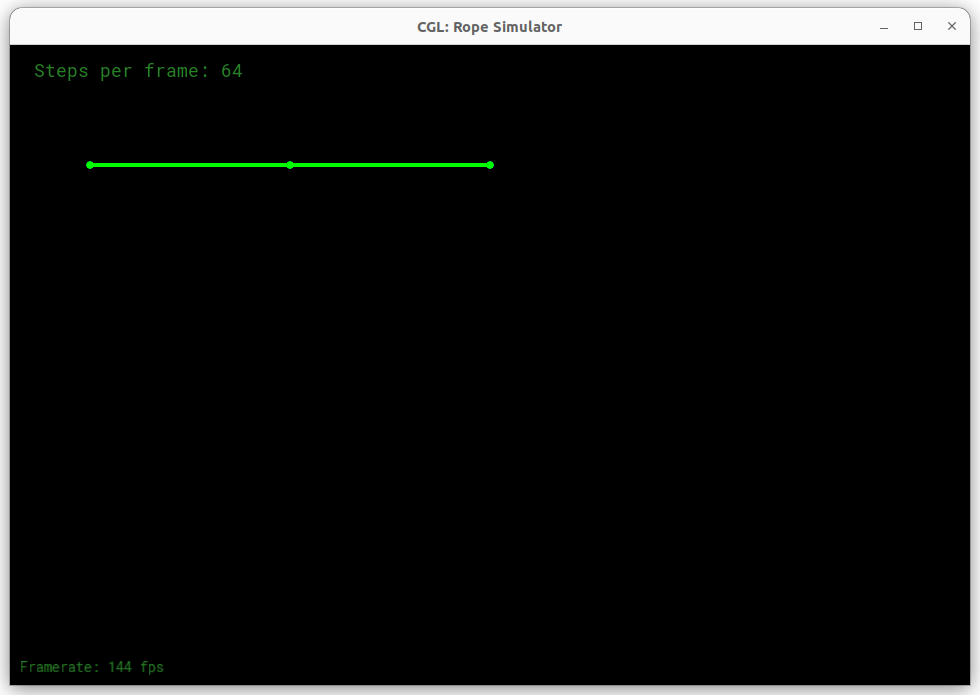
Rope::simulateEuler

// in rope.cpp
void Rope::simulateEuler(float delta_t, Vector2D gravity)
{
    for (auto &s : springs)
    {
        // TODO (Part 2): Use Hooke's law to calculate the force on a node
        Vector2D dis = s->m1->position - s->m2->position;// 两质量距离矢量，m2指向m1
        float curr_length = dis.norm();// 弹簧当前长度
        Vector2D force = s->k * (curr_length - s->rest_length) * dis / curr_length;// 对于m2的力矢量
        s->m1->forces -= force;
        s->m2->forces += force;
    }

    for (auto &m : masses)
    {
        if (!m->pinned)
        {
            // TODO (Part 2): Add the force due to gravity, then compute the new velocity and position
            m->forces += gravity * m->mass;// 加上重力
            Vector2D a = m->forces / m->mass;// 加速度a=F/m
            m->velocity += a * delta_t;
            m->position += m->velocity * delta_t;
            // TODO (Part 2): Add global damping
        }

        // Reset all forces on each mass
        m->forces = Vector2D(0, 0);
    }
}

首先利用胡克定律计算结点的受力（变量计算说明见注释），记得不要搞错方向。
在第二个for循环中遍历质点，加上重力，并计算加速度，以此更新速度与位置。

// in application.cpp
ropeEuler = new Rope(Vector2D(0, 200), Vector2D(-400, 200), 16, config.mass,
                        config.ks, {0});
ropeVerlet = new Rope(Vector2D(0, 200), Vector2D(-400, 200), 16, config.mass,
                        config.ks, {0});

3个结点太少，application.cpp中修改上述函数，将结点数量改为16个。

编译运行
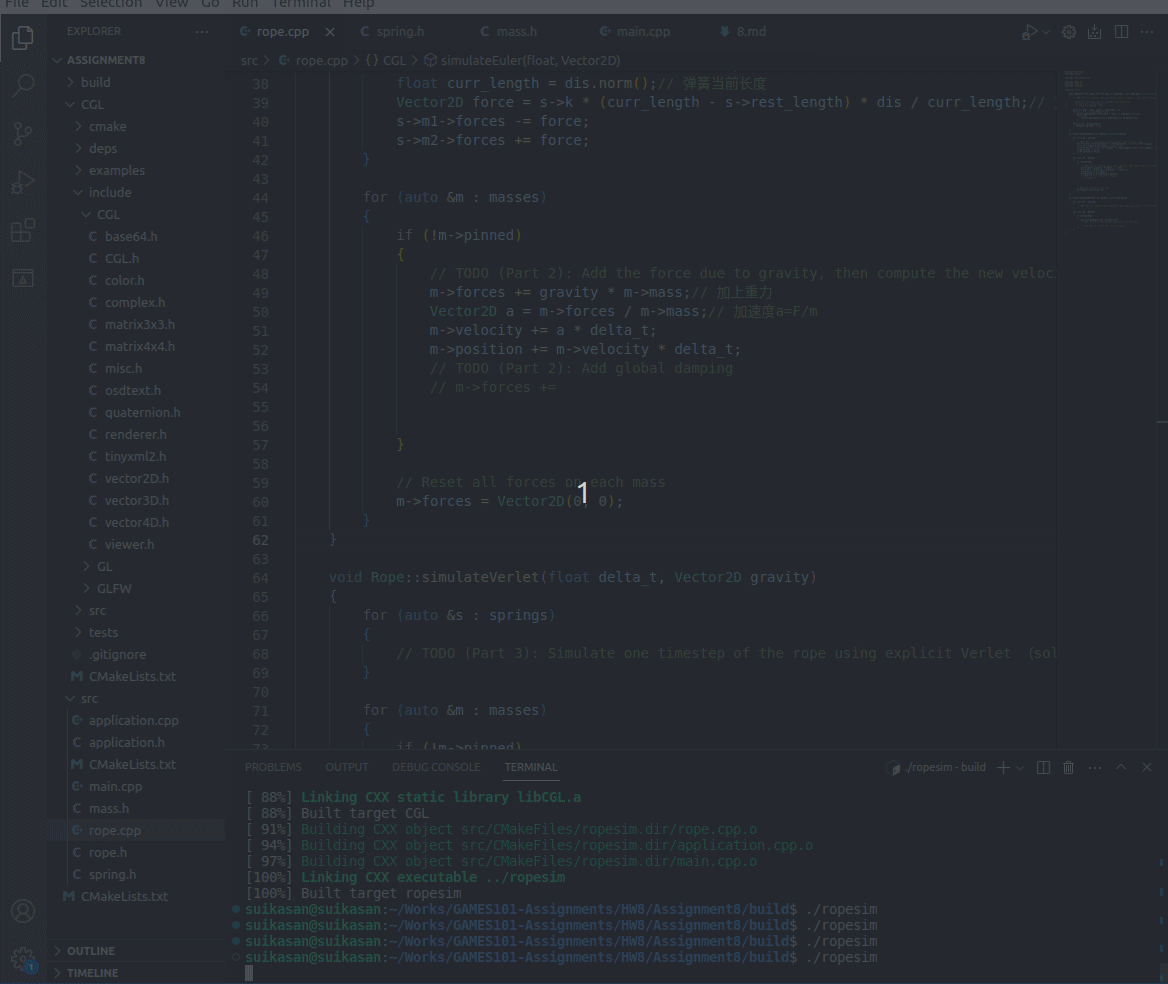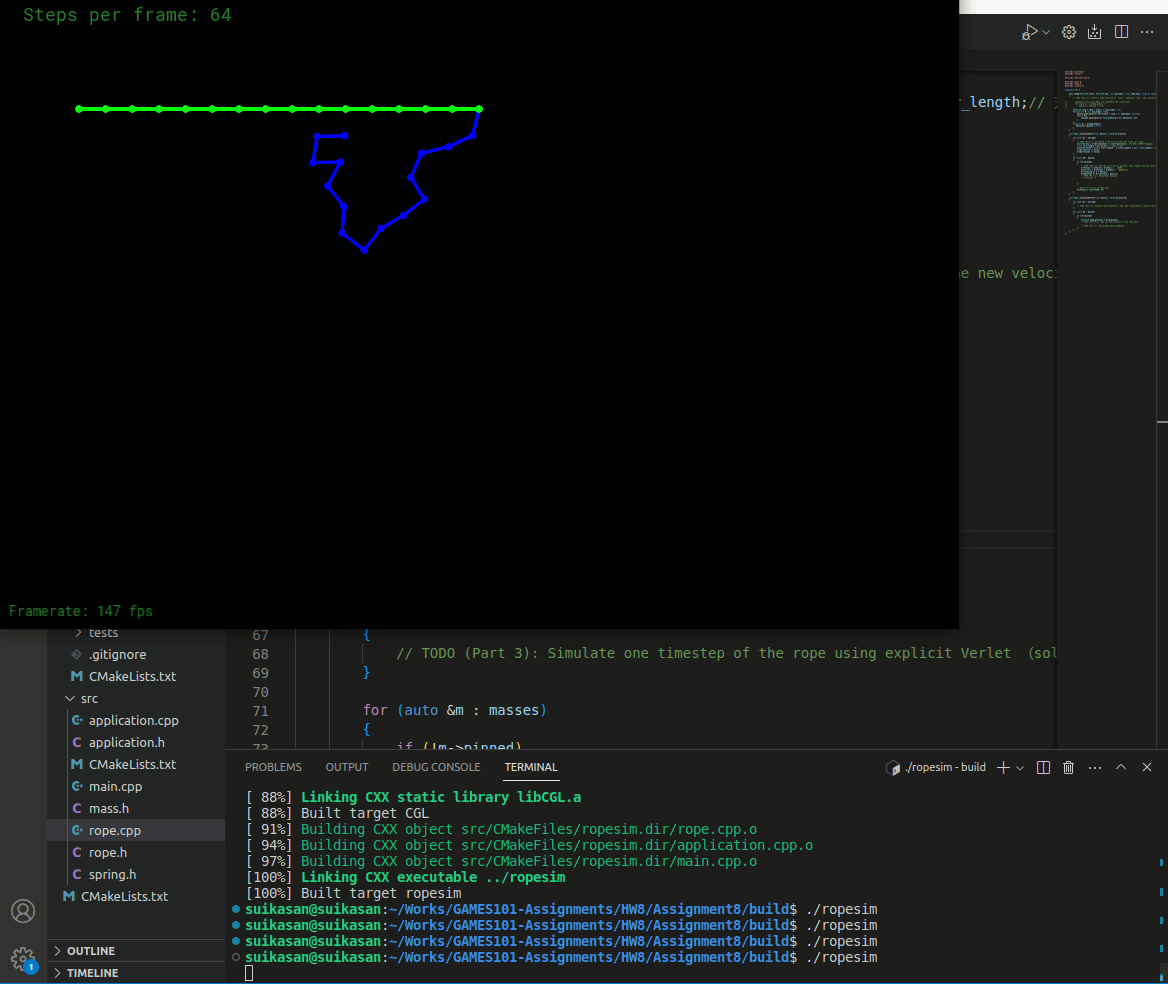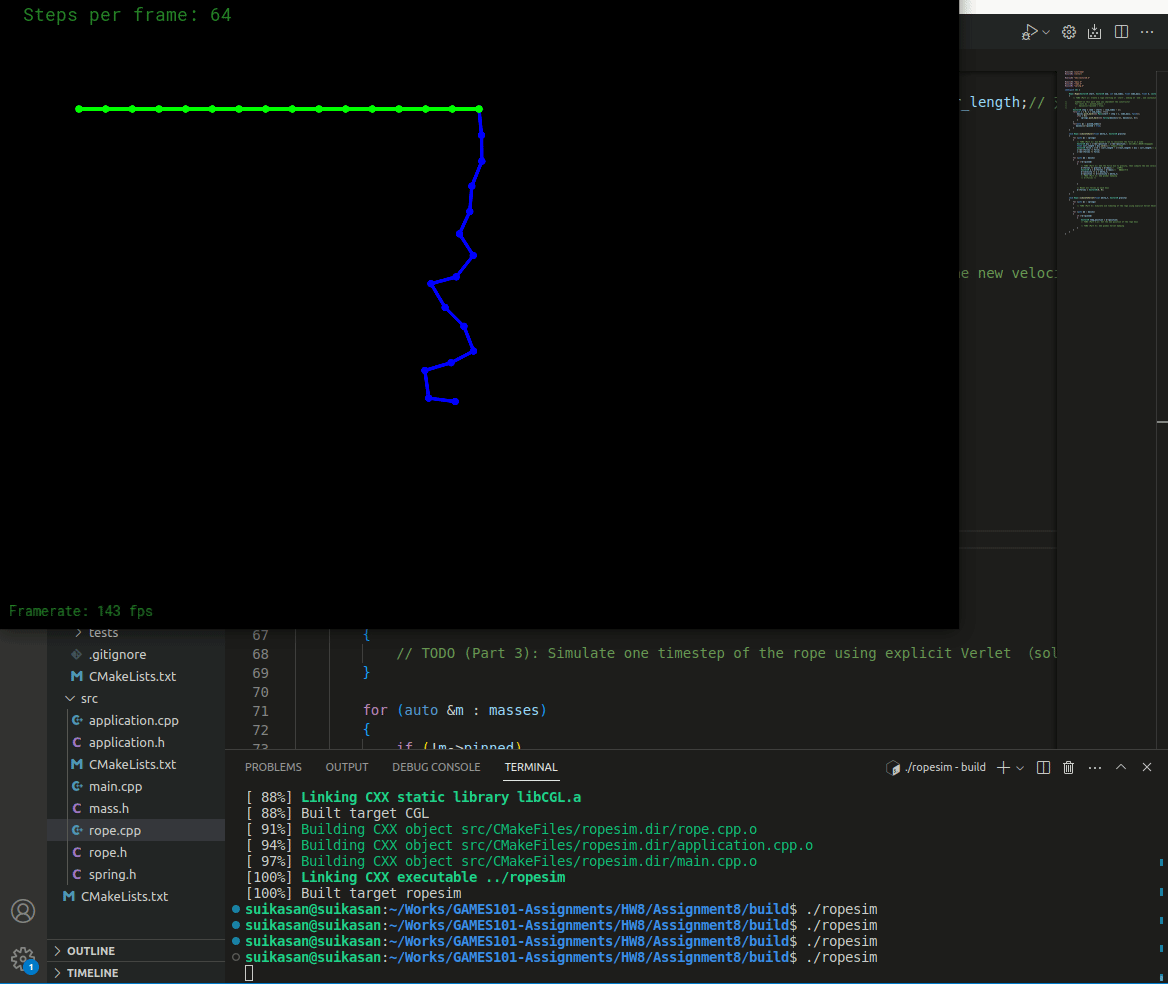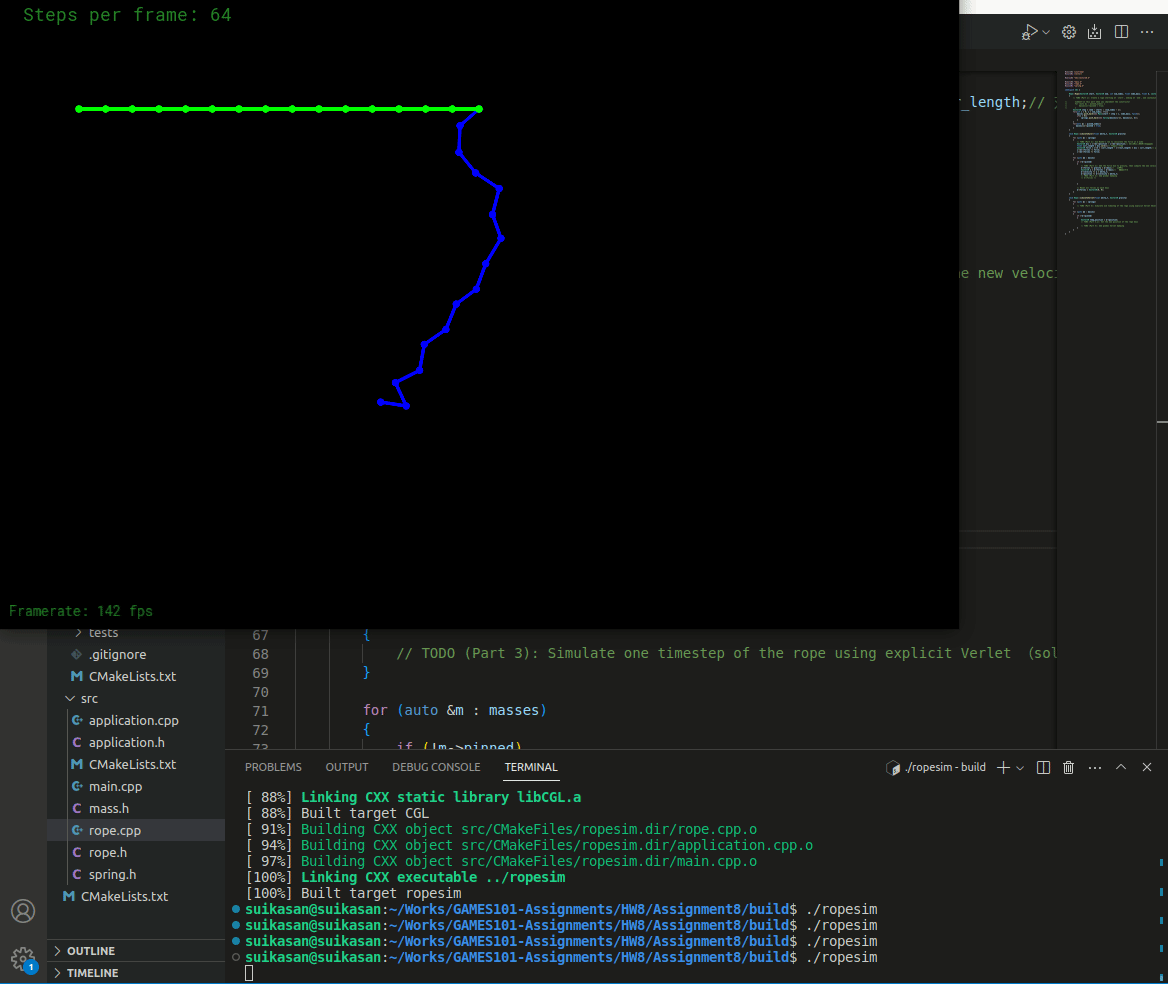
Euler
此时由于没有引入Damping，弹簧将永远不会停止运动，并且运动状态特别不稳定。

下面加入Damping，修改后的Rope::simulateEuler如下

// in rope.cpp
void Rope::simulateEuler(float delta_t, Vector2D gravity)
    {
        for (auto &s : springs)
        {
            ......

            // Internal Damping
            Vector2D D_V = s->m1->velocity - s->m2->velocity;
            Vector2D disNorm = dis / curr_length;
            float k_d = 0.05f;
            Vector2D force_a = -k_d * (disNorm.x * D_V.x + disNorm.y * D_V.y) * dis / curr_length;
            s->m1->forces += force_a;
            s->m2->forces -= force_a;
        }

        for (auto &m : masses)
        {
            ......
        }
    }

加入了Internal Damping，具体计算方法如Lecture 21中所述，其实就是套如下公式，唯一的区别是ppt中公式计算的力是对b点而言的，上面代码中则是先计算a点，即m1
InternalDampingFormula

编译运行结果如下
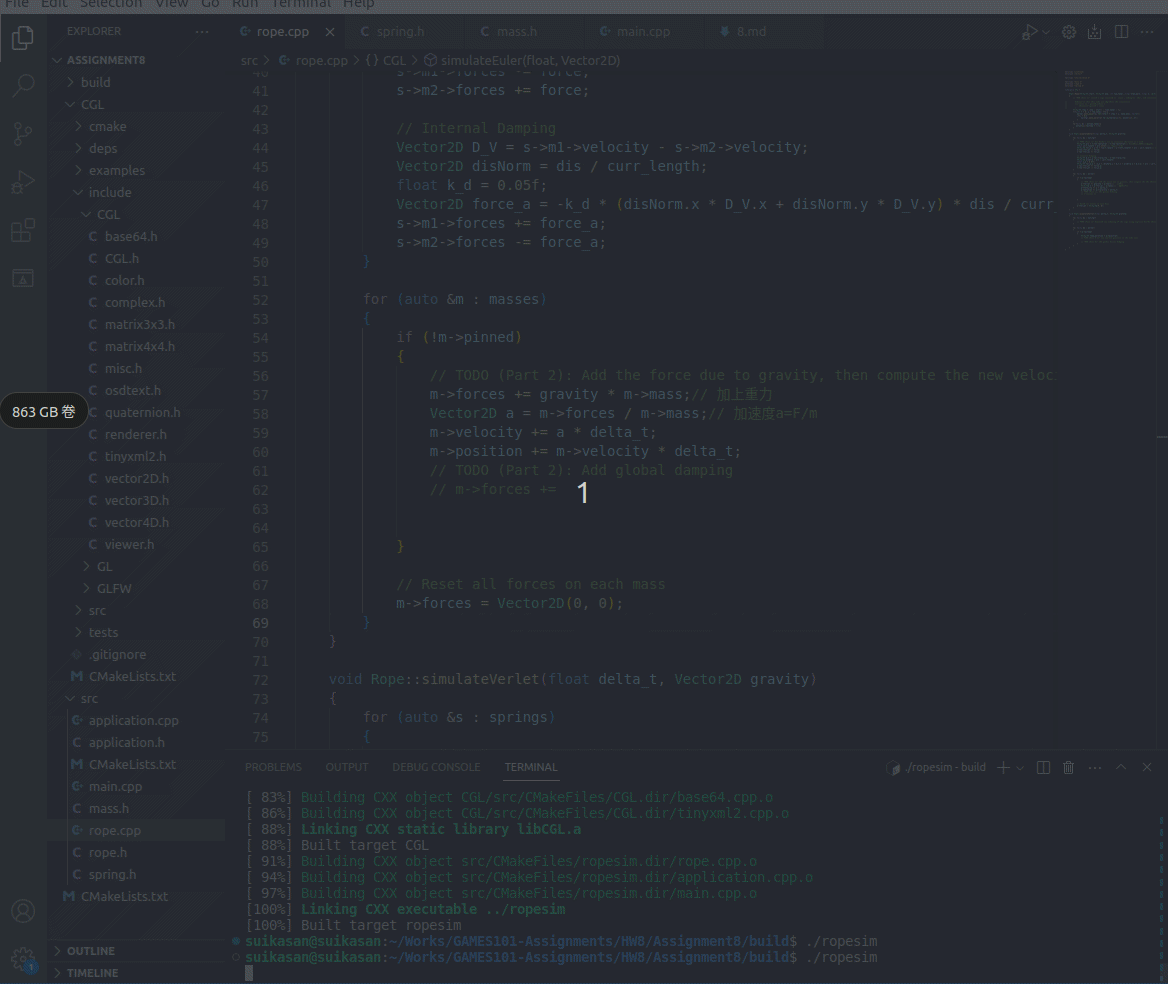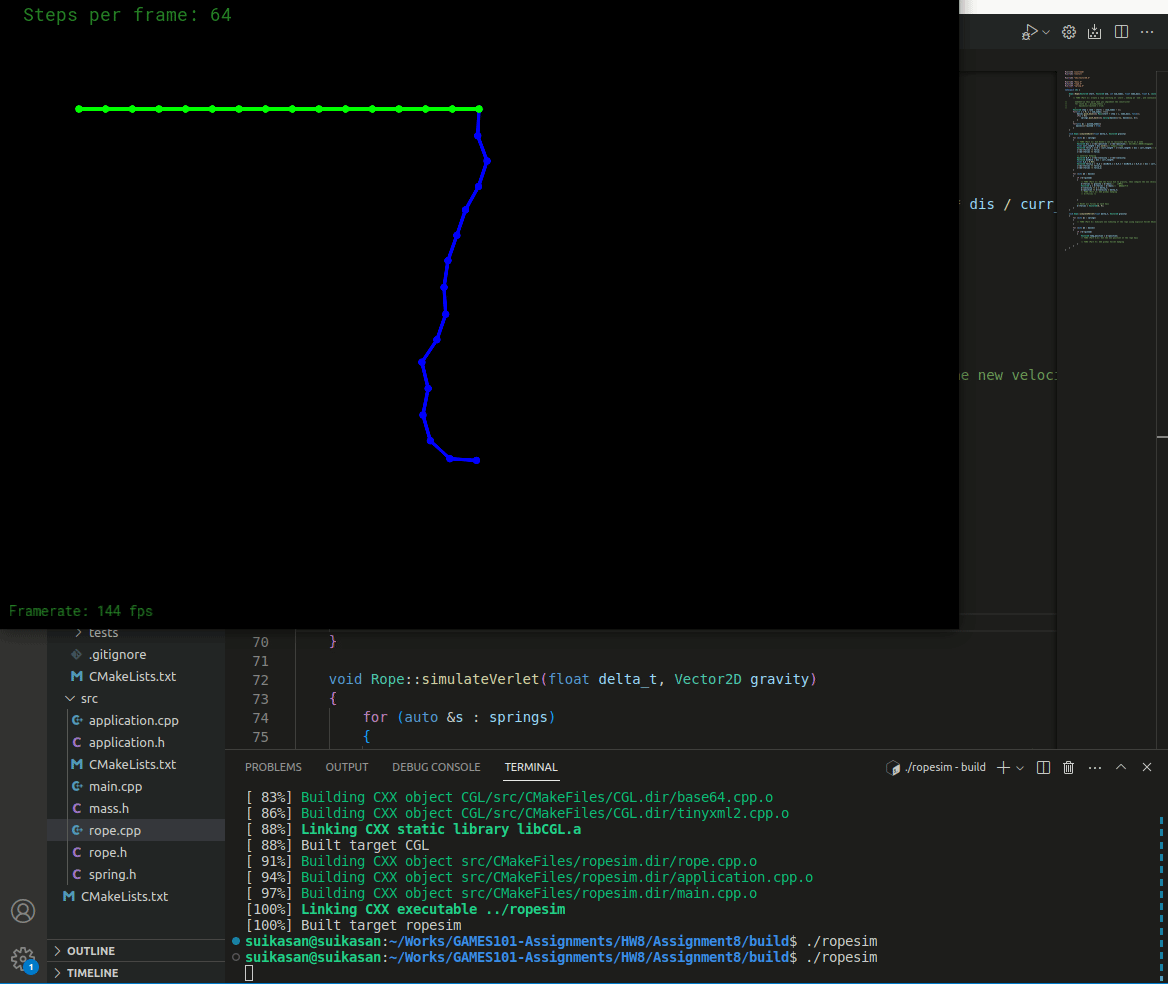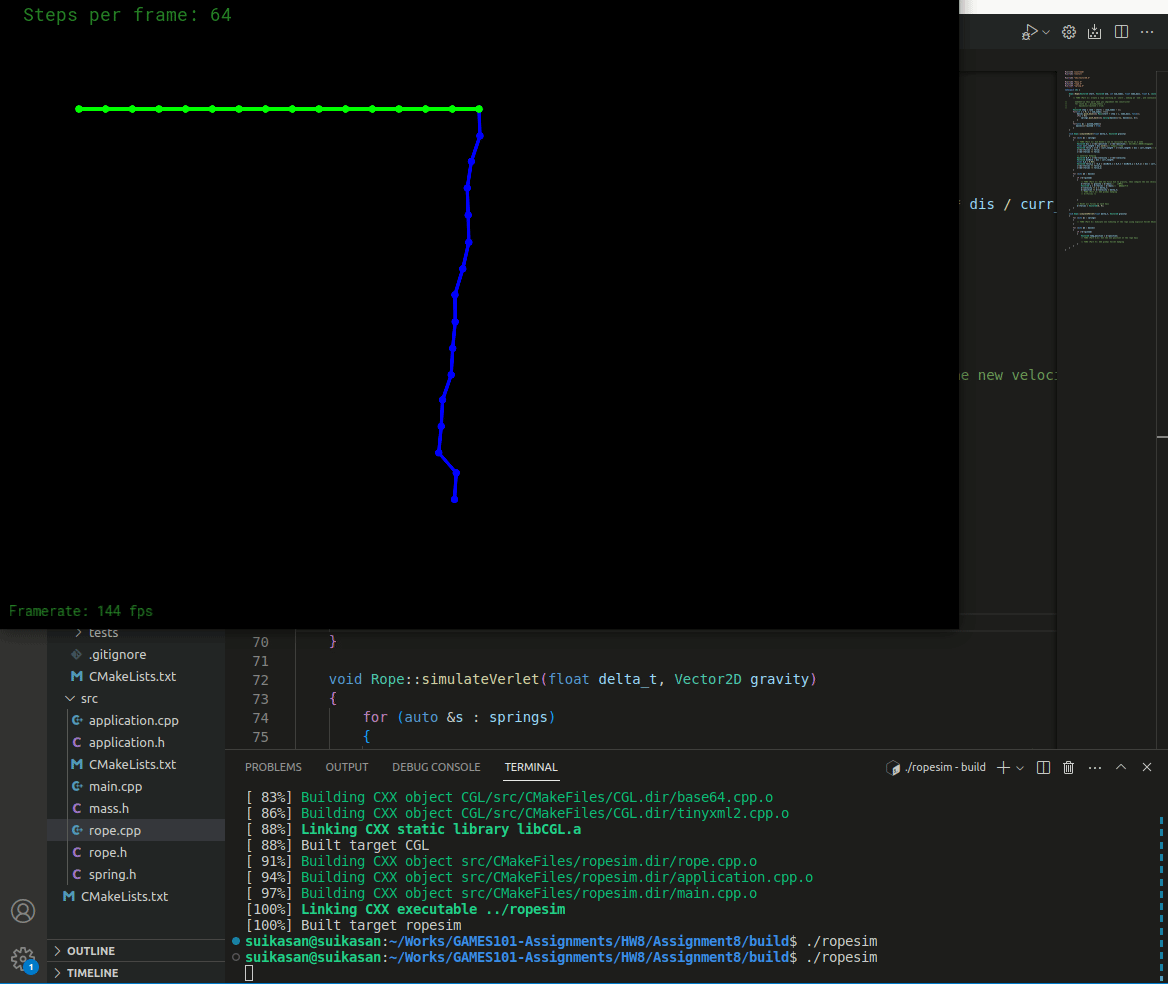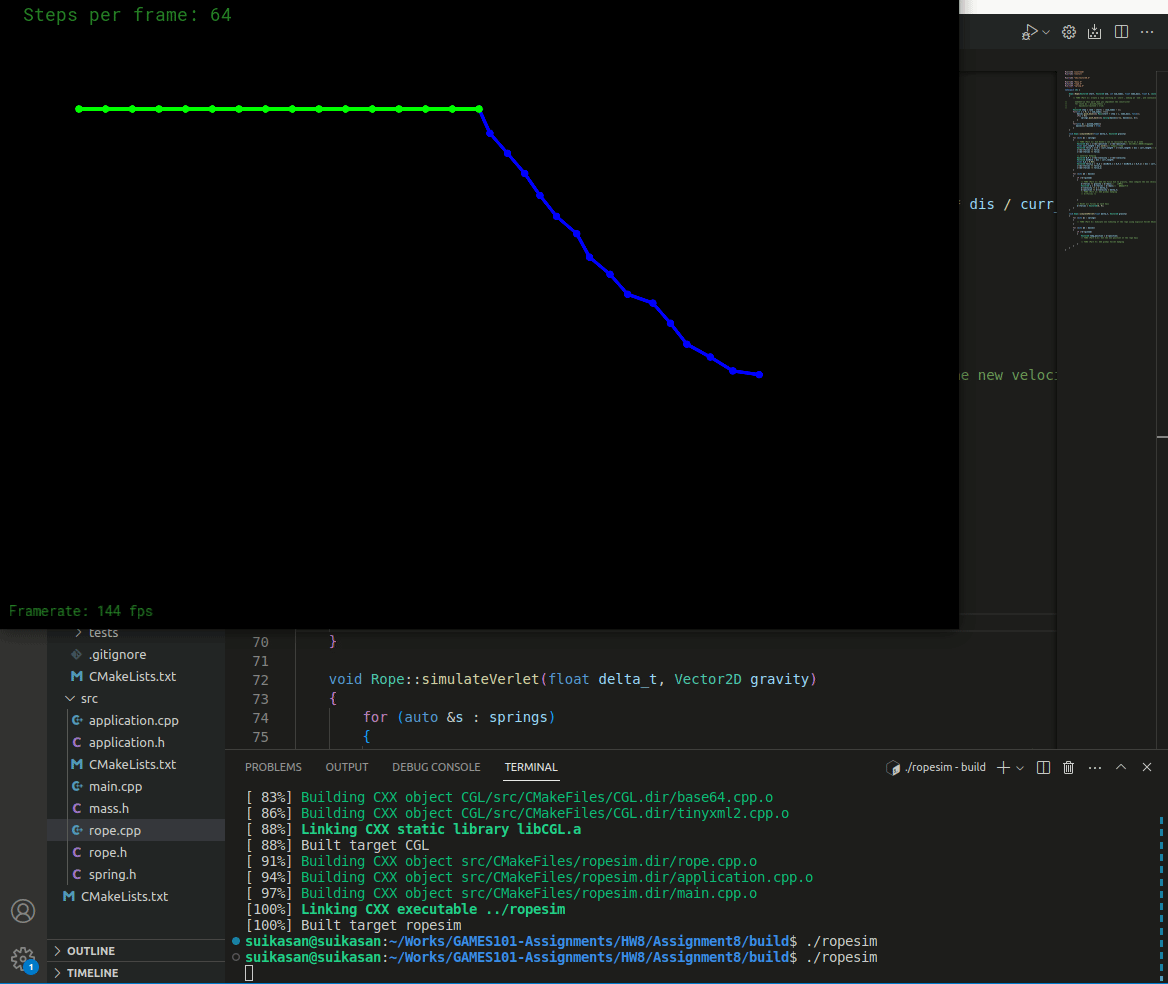
InternalDamping
可见弹簧的运动状态变得更加稳定，但是由于没有空气阻力，弹簧仍然不会静止

下面引入空气阻力

// in rope.cpp
void Rope::simulateEuler(float delta_t, Vector2D gravity)
    {
        for (auto &s : springs)
        {
            ......

            // Internal Damping
            Vector2D D_V = s->m1->velocity - s->m2->velocity;
            Vector2D disNorm = dis / curr_length;
            float k_d = 0.05f;
            Vector2D force_a = -k_d * (disNorm.x * D_V.x + disNorm.y * D_V.y) * dis / curr_length;
            s->m1->forces += force_a;
            s->m2->forces -= force_a;

            // Air Damping
            s->m1->forces += -0.005f * s->m1->velocity;
            s->m2->forces += -0.005f * s->m2->velocity;
        }

        for (auto &m : masses)
        {
            ......
        }
    }

编译运行
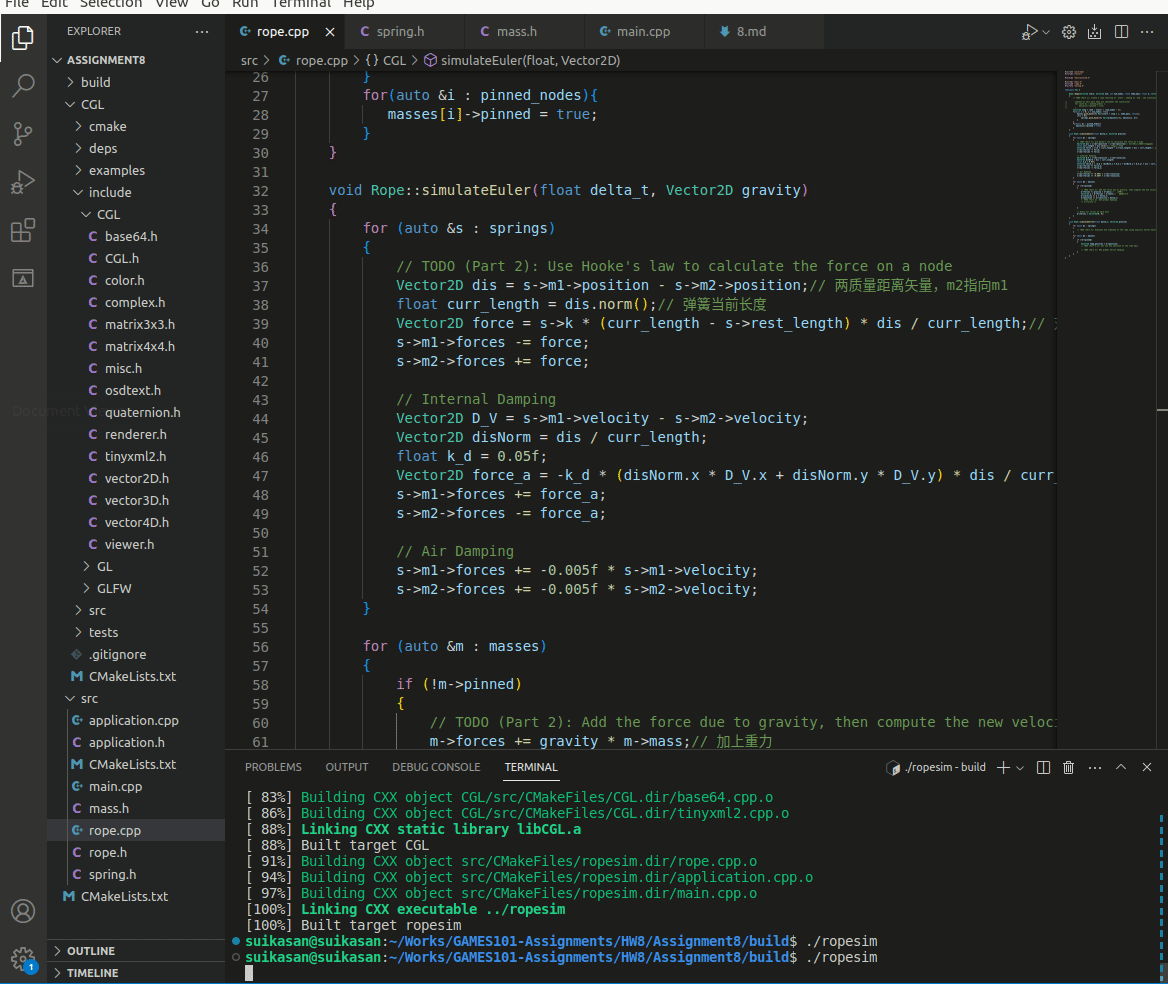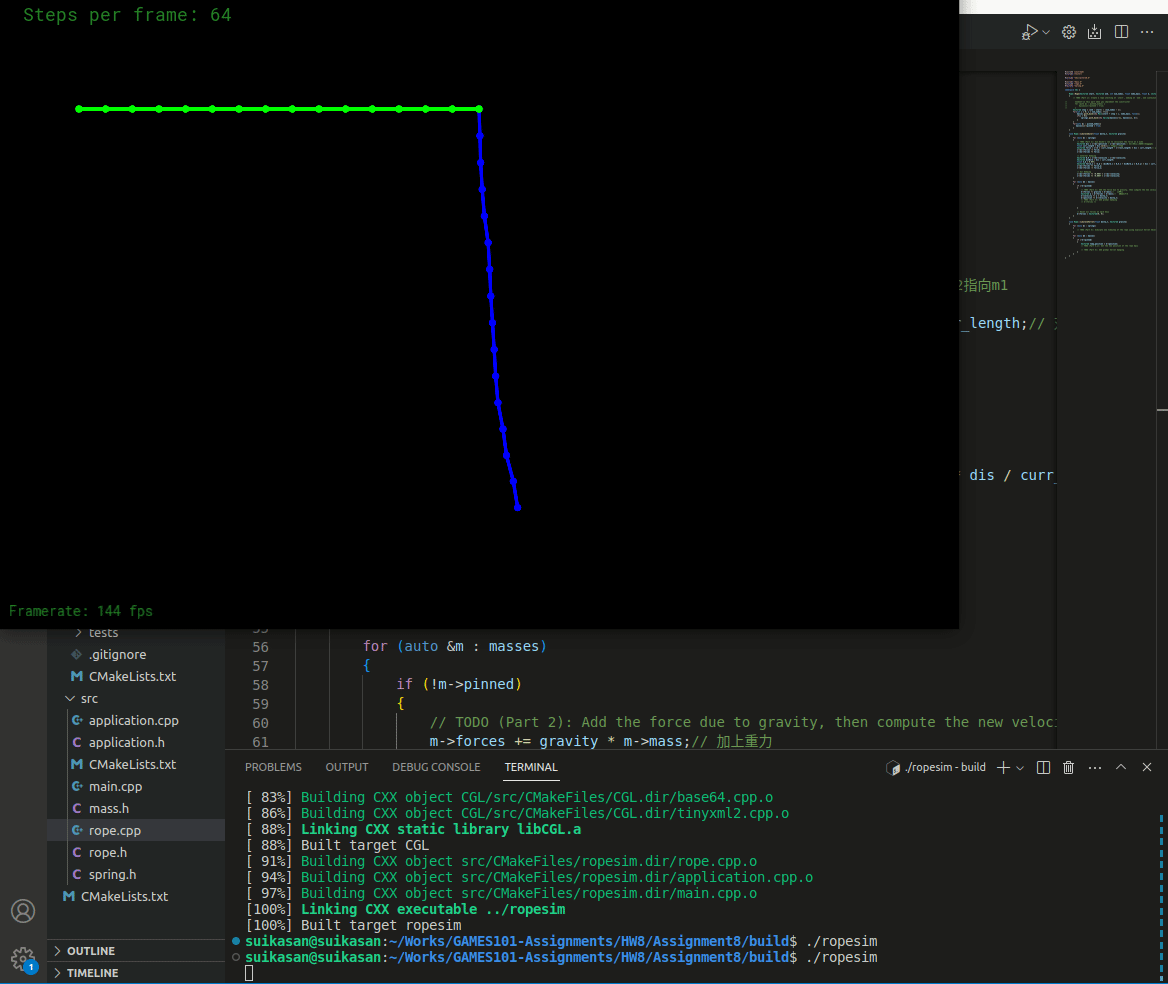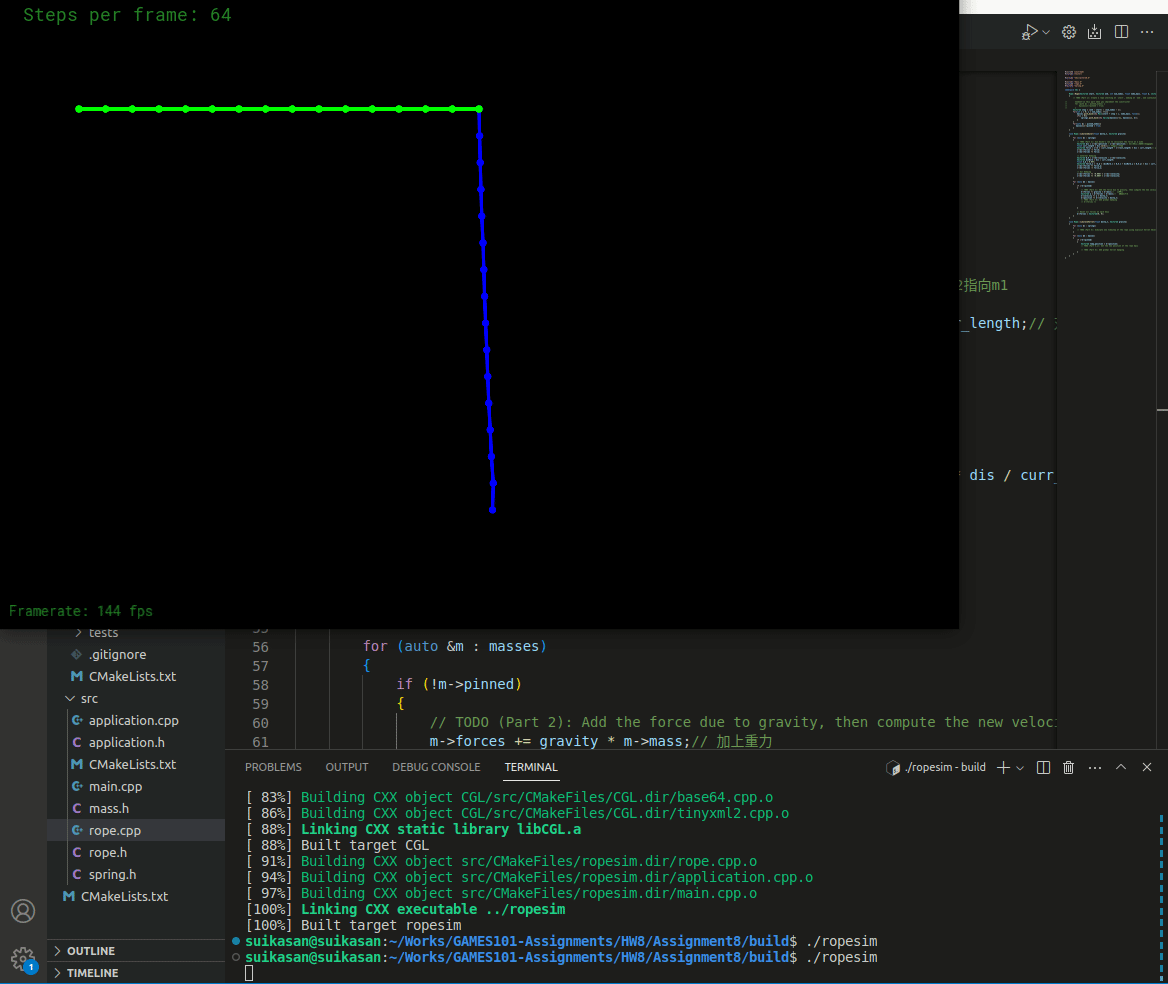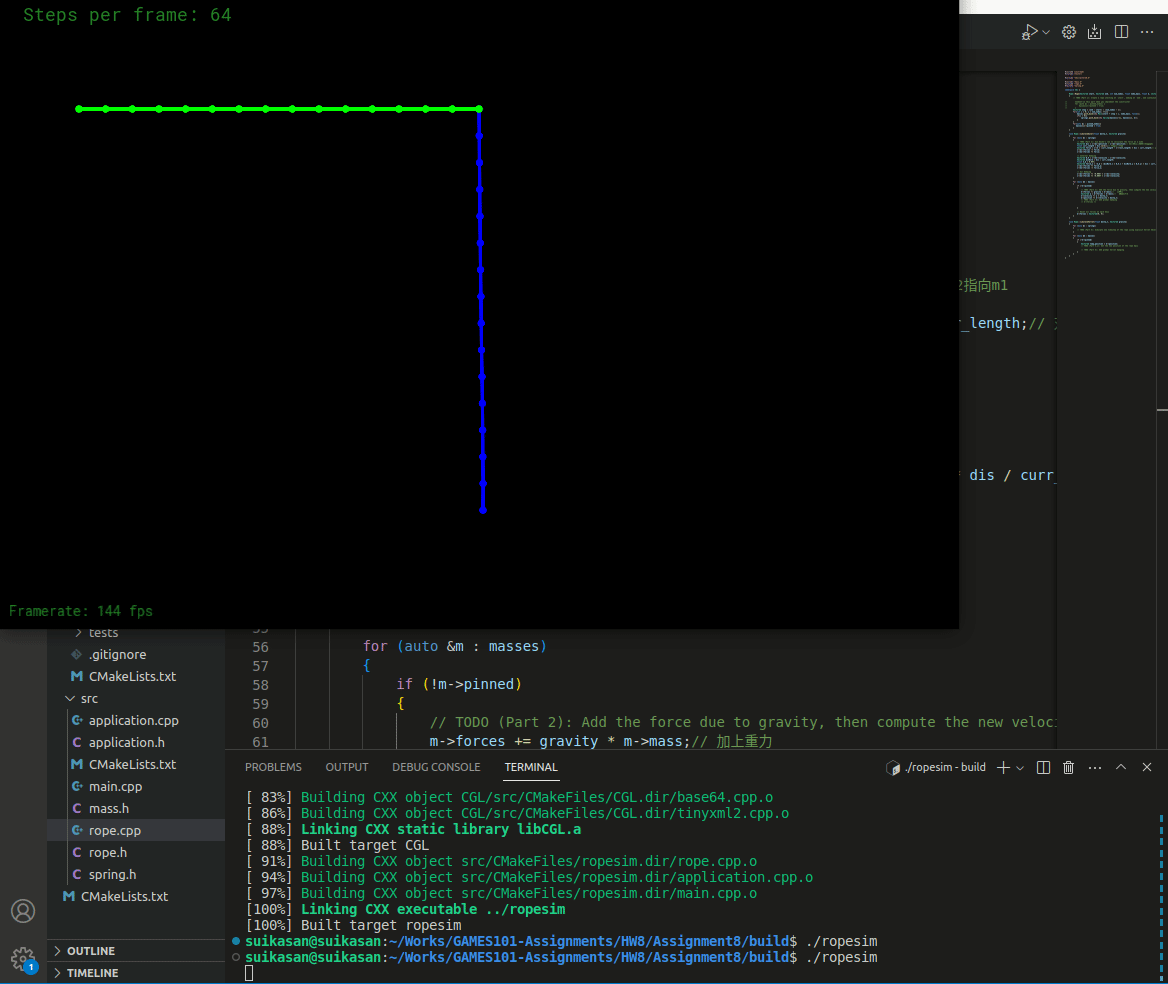
AirDamping
弹簧运动稳定且最终会静止

最终，完整的Rope::simulateEuler函数如下

// in rope.cpp
void Rope::simulateEuler(float delta_t, Vector2D gravity)
{
    for (auto &s : springs)
    {
        // TODO (Part 2): Use Hooke's law to calculate the force on a node
        Vector2D dis = s->m1->position - s->m2->position;// 两质量距离矢量，m2指向m1
        float curr_length = dis.norm();// 弹簧当前长度
        Vector2D force = s->k * (curr_length - s->rest_length) * dis / curr_length;// 对于m2的力矢量
        s->m1->forces -= force;
        s->m2->forces += force;

        // Internal Damping
        Vector2D D_V = s->m1->velocity - s->m2->velocity;
        Vector2D disNorm = dis / curr_length;
        float k_d = 0.05f;
        Vector2D force_a = -k_d * (disNorm.x * D_V.x + disNorm.y * D_V.y) * dis / curr_length;
        s->m1->forces += force_a;
        s->m2->forces -= force_a;

        // Air Damping
        s->m1->forces += -0.005f * s->m1->velocity;
        s->m2->forces += -0.005f * s->m2->velocity;
    }

    for (auto &m : masses)
    {
        if (!m->pinned)
        {
            // TODO (Part 2): Add the force due to gravity, then compute the new velocity and position
            // TODO (Part 2): Add global damping
            m->forces += gravity * m->mass;// 加上重力
            Vector2D a = m->forces / m->mass;// 加速度a=F/m
            m->velocity += a * delta_t;
            m->position += m->velocity * delta_t;
        }

        // Reset all forces on each mass
        m->forces = Vector2D(0, 0);
    }
}

Rope::simulateVerlet

// in rope.cpp
void Rope::simulateVerlet(float delta_t, Vector2D gravity)
{
    for (auto &s : springs)
    {
        // TODO (Part 3): Simulate one timestep of the rope using explicit Verlet （solving constraints)
        Vector2D dis = s->m1->position - s->m2->position;// 两质量距离矢量，m2指向m1
        float curr_length = dis.norm();// 弹簧当前长度
        Vector2D force = s->k * (curr_length - s->rest_length) * dis / curr_length;// 对于m2的力矢量
        s->m1->forces -= force;
        s->m2->forces += force;
    }

    for (auto &m : masses)
    {
        if (!m->pinned)
        {
            Vector2D temp_position = m->position;
            // TODO (Part 3.1): Set the new position of the rope mass
            m->forces += gravity * m->mass;
            Vector2D a = m->forces / m->mass;
            // TODO (Part 4): Add global Verlet damping
            float damping_factor = 0.00005;
            m->position = m->position + (1 - damping_factor) * (m->position - m->last_position)
                            + a * delta_t * delta_t;
            m->last_position = temp_position;
        }
        m->forces = Vector2D(0,0);
    }
}

前面与欧拉法一致，根据如下公式

x(t+1) = x(t) + (1 - damping_factor) * [x(t)-x(t-1)] + a(t) * dt * dt

进行模拟，并引入阻尼

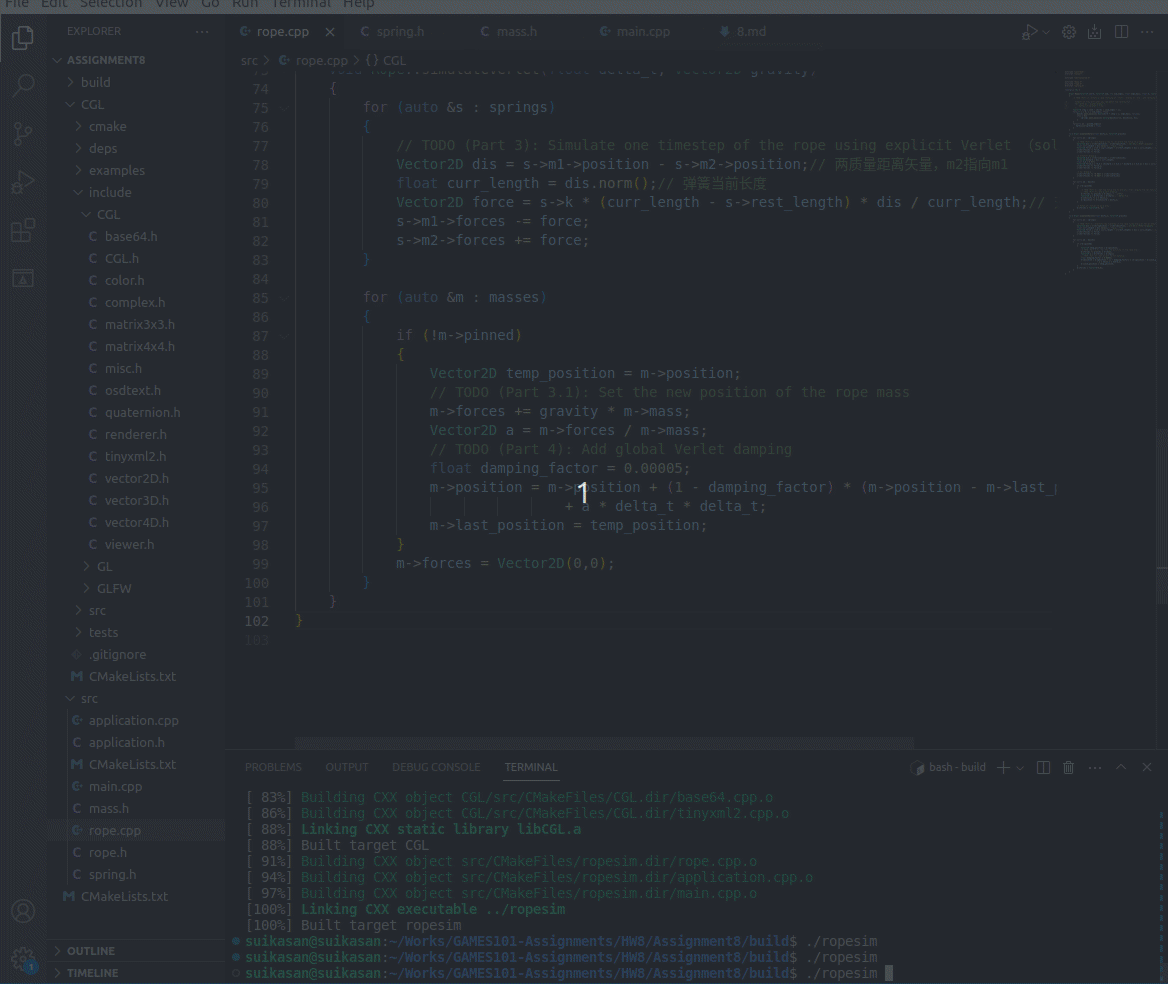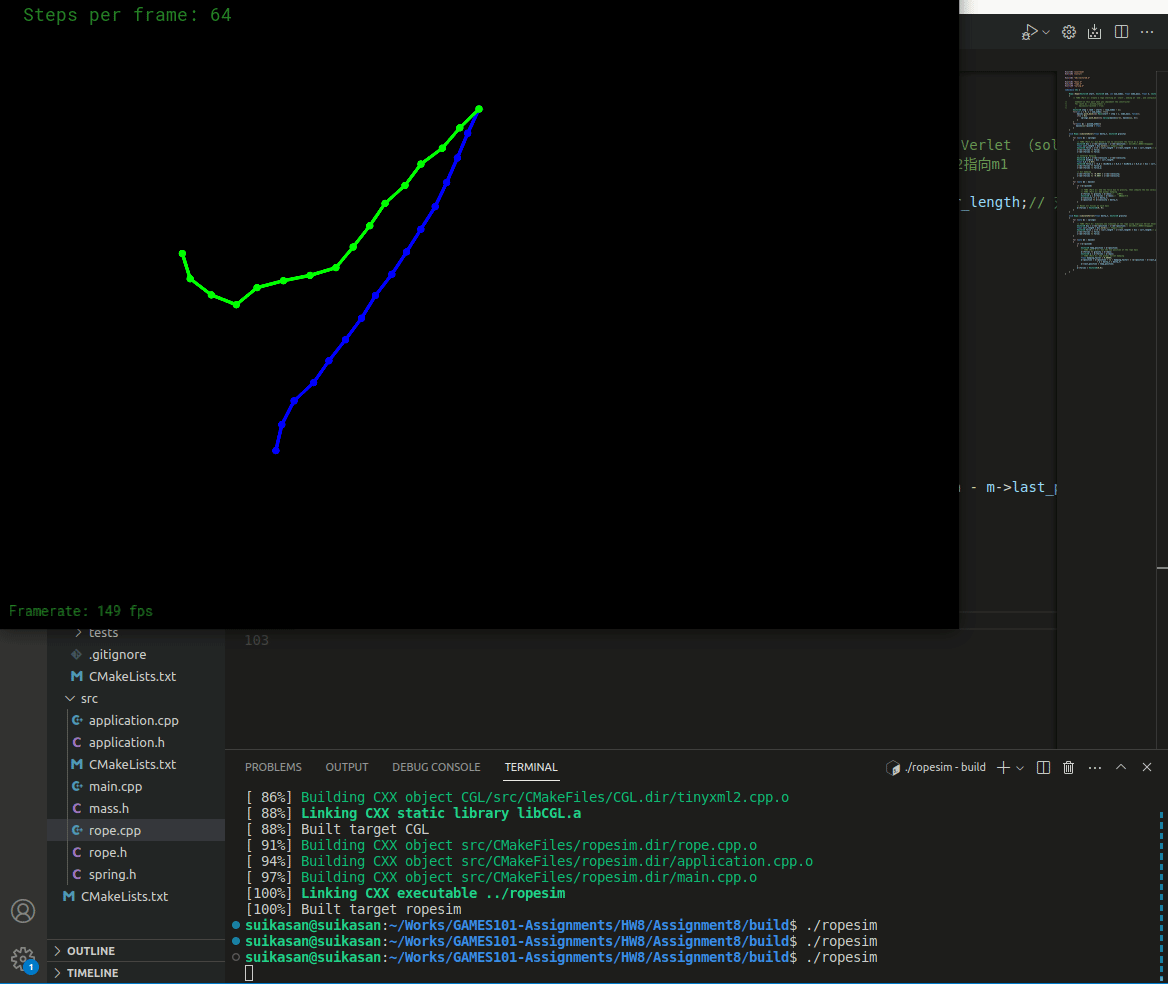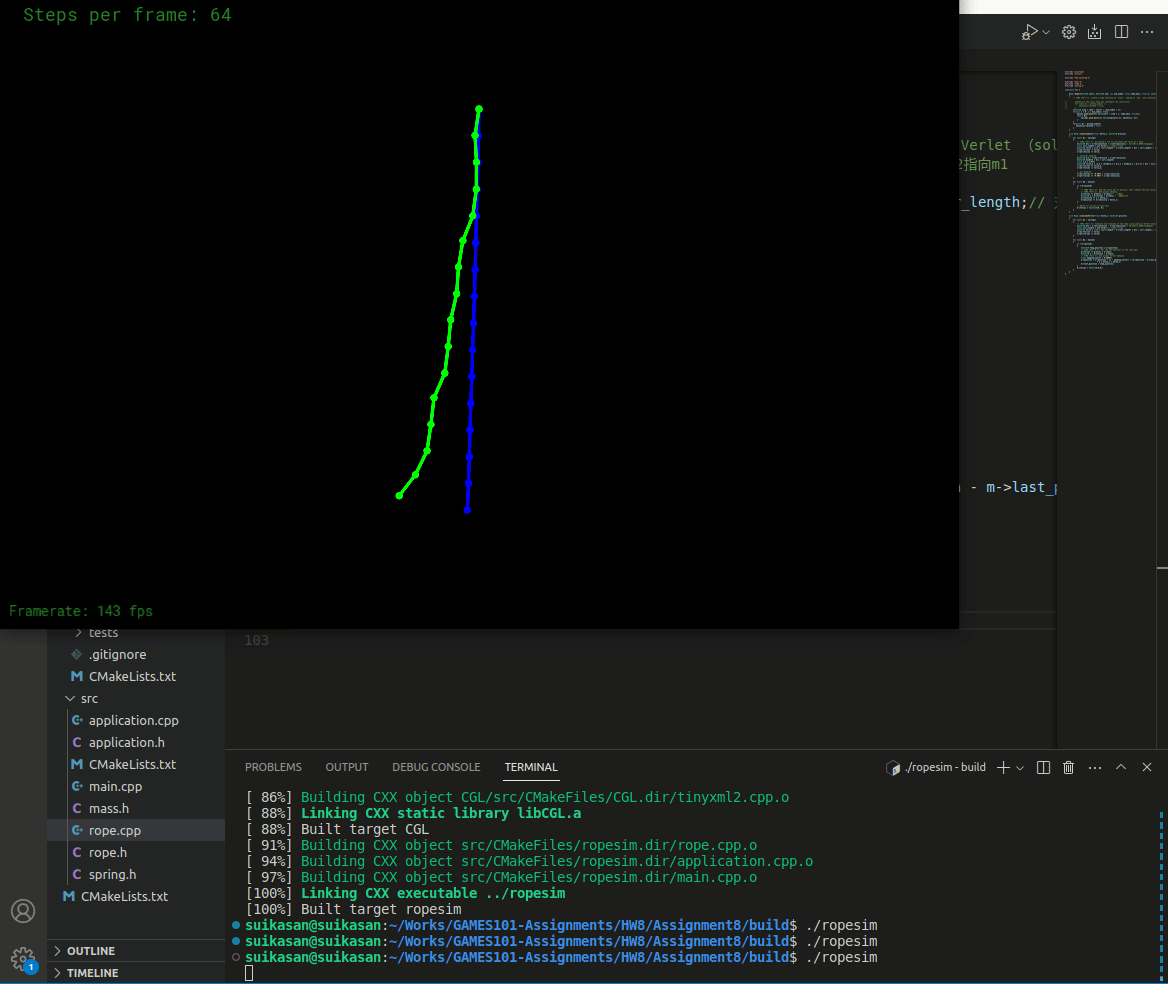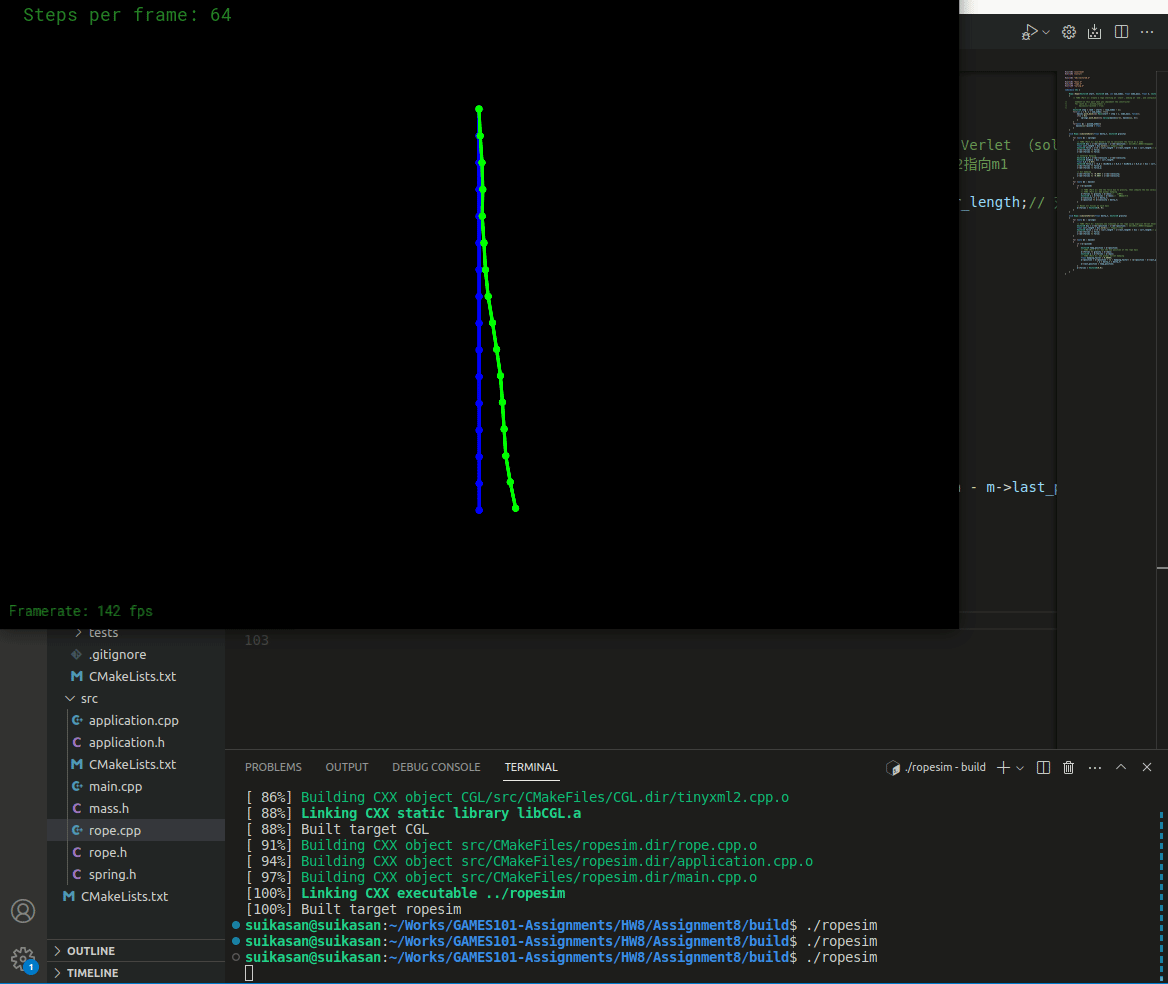
结果如下
Verlet