前言
GAMES101作业系列为GAMES101作业记录(包含作业1-8),文章中会解释作业内容并附上代码,同时对代码框架进行简要说明。
已完成的代码可在我的GitHubGAMES101作业代码仓库获取。
GAMES101课程相关基础知识可参看本博客GAMES101知识梳理系列。
作业描述
本次作业重点关注物体划分算法Bounding Volume Hierarchy(BVH),在作业5的基础上实现Ray-Bounding Volume求交与BVH查找。
主要工作如下:
- 从上一次编程练习中引用以下函数:
- Render() in Renderer.cpp: 将你的光线生成过程粘贴到此处,并且按照新框架更新相应调用的格式;
- Triangle::getIntersection in Triangle.hpp: 将你的光线-三角形相交函数粘贴到此处,并且按照新框架更新相应相交信息的格式。
- 实现以下函数:
- IntersectP(const Ray& ray, const Vector3f& invDir, const std::array<int, 3>& dirIsNeg) in the Bounds3.hpp: 这个函数的作用是判断包围盒 BoundingBox 与光线是否相交,你需要按照课程介绍的算法实现求交过程;
- getIntersection(BVHBuildNode* node, const Ray ray)in BVH.cpp: 建立BVH之后,我们可以用它加速求交过程。该过程递归进行,你将在其中调用你实现的 Bounds3::IntersectP.
完成作业
Render
// in Renderer.cpp
void Renderer::Render(const Scene& scene)
{
std::vector<Vector3f> framebuffer(scene.width * scene.height);
float scale = tan(deg2rad(scene.fov * 0.5));
float imageAspectRatio = scene.width / (float)scene.height;
Vector3f eye_pos(-1, 5, 10);
int m = 0;
for (uint32_t j = 0; j < scene.height; ++j) {
for (uint32_t i = 0; i < scene.width; ++i) {
// generate primary ray direction
// TODO: Find the x and y positions of the current pixel to get the
// direction
// vector that passes through it.
// Also, don't forget to multiply both of them with the variable
// *scale*, and x (horizontal) variable with the *imageAspectRatio*
// Don't forget to normalize this direction!
float x, y;
x = 2 * scale * imageAspectRatio / scene.width * (i + 0.5f) - scale * imageAspectRatio;
y = -2 * scale / scene.height * (j + 0.5f) + scale;
Vector3f dir = Vector3f(x, y, -1); // Don't forget to normalize this direction!
dir = normalize(dir);
Ray ray(eye_pos, dir);
framebuffer[m++] = scene.castRay(ray, 0);
}
UpdateProgress(j / (float)scene.height);
}
UpdateProgress(1.f);
// save framebuffer to file
FILE* fp = fopen("binary.ppm", "wb");
(void)fprintf(fp, "P6\n%d %d\n255\n", scene.width, scene.height);
for (auto i = 0; i < scene.height * scene.width; ++i) {
static unsigned char color[3];
color[0] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].x));
color[1] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].y));
color[2] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].z));
fwrite(color, 1, 3, fp);
}
fclose(fp);
}这次需要使用新增加的Ray类,用eye_pos和dir构造,传入castRay即可。
Triangle::getIntersection
// in Triangle.hpp
inline Intersection Triangle::getIntersection(Ray ray)
{
Intersection inter;
if (dotProduct(ray.direction, normal) > 0)
return inter;
double u, v, t_tmp = 0;
Vector3f pvec = crossProduct(ray.direction, e2);
double det = dotProduct(e1, pvec);
if (fabs(det) < EPSILON)
return inter;
double det_inv = 1. / det;
Vector3f tvec = ray.origin - v0;
u = dotProduct(tvec, pvec) * det_inv;
if (u < 0 || u > 1)
return inter;
Vector3f qvec = crossProduct(tvec, e1);
v = dotProduct(ray.direction, qvec) * det_inv;
if (v < 0 || u + v > 1)
return inter;
t_tmp = dotProduct(e2, qvec) * det_inv;
// TODO find ray triangle intersection
inter.coords = ray(t_tmp);//将相交时间t_tmp传给Ray的函数调用运算符,算得交点
inter.distance = t_tmp;
inter.happened = true;
inter.m = this->m;
inter.normal = this->normal;
inter.obj = this;
return inter;
}光线和三角形求交代码框架中其实已经实现,我们需要做的就是正确地将相交信息赋值给inter。
IntersectP
// in Bounds3.hpp
inline bool Bounds3::IntersectP(const Ray& ray, const Vector3f& invDir,
const std::array<int, 3>& dirIsNeg) const
{
// invDir: ray direction(x,y,z), invDir=(1.0/x,1.0/y,1.0/z), use this because Multiply is faster that Division
// dirIsNeg: ray direction(x,y,z), dirIsNeg=[int(x>0),int(y>0),int(z>0)], use this to simplify your logic
// TODO test if ray bound intersects
Vector3f tMin = (this->pMin - ray.origin) * invDir;
Vector3f tMax = (this->pMax - ray.origin) * invDir;
if(dirIsNeg[0])
std::swap(tMin.x, tMax.x);
if(dirIsNeg[1])
std::swap(tMin.y, tMax.y);
if(dirIsNeg[2])
std::swap(tMin.z, tMax.z);
float tEnter, tExit;
tEnter = std::max(tMin.x, std::max(tMin.y, tMin.z));
tExit = std::min(tMax.x, std::min(tMax.y, tMax.z));
if(tEnter < tExit && tExit > 0)
return true;
return false;
}根据课程中所述的方法进行光线与包围盒的求交。
其中函数的参数需要注意:
- invDir是光线坐标的倒数,用于计算相交时间,因为乘法比除法快,所以提前计算好倒数;
- dirIsNeg用于判断光线是否为反向,由于我们默认光线为正向进行计算,所以如果是反方向就需要将对应坐标上的相交时间对换。dirIsNeg的三个值分别表示光线在x,y,z上是否为反向,1表示反向,0表示正向,使用该函数前要注意其参数的构造。
getIntersection
// in BVH.cpp
Intersection BVHAccel::getIntersection(BVHBuildNode* node, const Ray& ray) const
{
// TODO Traverse the BVH to find intersection
Intersection inter, interL, interR;
Vector3f invDir(ray.direction_inv);
std::array<int, 3> dirIsNeg;
dirIsNeg[0] = ray.direction.x < 0;
dirIsNeg[1] = ray.direction.y < 0;
dirIsNeg[2] = ray.direction.z < 0;
// 光线与当前包围盒没有交点
if(!node->bounds.IntersectP(ray, invDir, dirIsNeg))
return inter;
// 光线与当前包围盒有交点且包围盒是叶子节点
else if(node->left == nullptr && node->right == nullptr){
inter = node->object->getIntersection(ray);
return inter;
}
// 光线与包围盒有交点且包围盒是中间节点
else{
interL = getIntersection(node->left, ray);
interR = getIntersection(node->right, ray);
return interL.distance < interR.distance ? interL : interR;
}
}实现BVH的遍历,分成三种包围盒情况:
- 如果没有交点则直接返回当前inter;
- 如果有交点,但是该包围盒没有左右子节点(即该节点为叶子节点),光线与当前包围盒内物体求交;
- 如果有交点,且包围盒有左右子节点,则对子节点分别递归遍历求交,递归至最后会回到1或2两种情况,然后遍历结束。
效果

SAH(提高)
注:提高部分参考了csdn作者ycr的帐号的文章:【GAMES101】作业6(提高)含BVH与SAH加速查找算法(SVH)和快速排序算法
根据作业文档给出的链接,我们可以得到表面积启发式算法(Surface Area Heuristic, SAH)的公式:
下面对公式进行简要解释
其中,为遍历到当前包围盒的开销,为光线与单个物体相交计算的开销。和为子包围盒A,B内物体数量。和为光线通过子包围盒A和子包围盒B的概率,这个概率通过子包围盒A,B的表面积与当前节点包围盒表面积的比值表示,表面积启发式也是得名于此。
在实际遍历过程中,由于我们是对当前遍历到的包围盒进行划分选择,因此对当前包围盒始终是一个定值,可以略去。除此之外,我们认为也是确定的常数值,即认为对每个三角形的相交计算的开销都是相同的,因此也可以略去。
综上所述,我们在实现SAH时使用的其实是简化后的公式:
下面进行代码实现
// in BVH.cpp
BVHBuildNode* BVHAccel::recursiveBuildSAH(std::vector<Object*> objects){
BVHBuildNode* node = new BVHBuildNode();
// Compute bounds of all primitives in BVH node
Bounds3 bounds;
for (int i = 0; i < objects.size(); ++i)
bounds = Union(bounds, objects[i]->getBounds()); //读取每个三角形的包围盒并逐一合并成大包围盒
// 只有一个物体,则该物体就是叶子节点
if (objects.size() == 1) {
// Create leaf _BVHBuildNode_
node->bounds = objects[0]->getBounds();
node->object = objects[0];
node->left = nullptr;
node->right = nullptr;
return node;
}
// 有两个物体,则这两个物体是根节点的左右叶子节点
else if (objects.size() == 2) {
node->left = recursiveBuildSAH(std::vector{objects[0]});
node->right = recursiveBuildSAH(std::vector{objects[1]});
node->bounds = Union(node->left->bounds, node->right->bounds);
return node;
}
else{
auto beginning = objects.begin();
auto ending = objects.end();
if(objects.size() < 12){
auto middling = objects.begin() +objects.size() / 2;
auto leftshapes = std::vector<Object*>(beginning, middling);
auto rightshapes = std::vector<Object*>(middling, ending);
node->left = recursiveBuildSAH(leftshapes);
node->right = recursiveBuildSAH(rightshapes);
node->bounds = Union(node->left->bounds, node->right->bounds);
}
else{
Bounds3 centroidBounds;
// 将每个物体的包围盒的中心作为顶点构建大包围盒
for (int i = 0; i < objects.size(); ++i)
centroidBounds =
Union(centroidBounds, objects[i]->getBounds().Centroid());
int dim = centroidBounds.maxExtent();//判断哪个是最长轴(1-x,2-y,3-z)
// 根据最长轴,将物体按照对应轴坐标从小到大排序
switch (dim) {
case 0:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().x <
f2->getBounds().Centroid().x;
});
break;
case 1:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().y <
f2->getBounds().Centroid().y;
});
break;
case 2:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().z <
f2->getBounds().Centroid().z;
});
break;
}
auto size = objects.size();
int splitPosNum = 10;
int finalSplitPos = 0;
double mincost = __DBL_MAX__;
for(int i = 1; i < splitPosNum; ++i)
{
auto middling = objects.begin() + size * i / splitPosNum;
auto leftshapes = std::vector<Object*>(beginning, middling);
auto rightshapes = std::vector<Object*>(middling, ending);
assert(objects.size() == leftshapes.size() + rightshapes.size());
double leftSA = computeSurfaceArea(leftshapes);
double rightSA = computeSurfaceArea(rightshapes);
double S = leftSA + rightSA;
auto cost = leftSA / S * leftshapes.size() + rightSA / S * rightshapes.size();
if(cost < mincost){
mincost = cost;
finalSplitPos = i;
}
}
auto middling = objects.begin() + size * finalSplitPos / splitPosNum;
auto leftshapes = std::vector<Object*>(beginning, middling);
auto rightshapes = std::vector<Object*>(middling, ending);
assert(objects.size() == leftshapes.size() + rightshapes.size());
node->left = recursiveBuildSAH(leftshapes);
node->right = recursiveBuildSAH(rightshapes);
node->bounds = Union(node->left->bounds, node->right->bounds);
}
return node;
}
}SAH的实现中,对于只有一个或者两个物体的情况,其递归构建方式与之前相同,直接复制recursiveBuild函数中的实现即可。
对于物体数量大于2的情况,如前面注明的文章中ycr大佬所述,要先判断物体数量是否小于12,如果小于12则直接用和原来相同的中分法,否则再使用SAH方法。
这里的道理就是,对于物体数量小于12的情况,包围盒本身就不会太大,就算直接中分法也不会太影响构建出的BVH树的平衡,遍历速度不会因为这点影响而显著下降;相反,如果对于小于12的情况仍然使用SAH算法,虽然其保证了建树质量提高了遍历速度,但是由于SAH本身的计算开销,建树过程就较长,此时加速遍历的收益小于建树的额外开销。
注:此处为什么选择12作为阈值ycr大佬并未进行解释,是测试得到的值、算得的值还是单纯随手取一个较小的数量,暂时不得而知。
recursiveBuildSAH中需要计算左右子包围盒的面积用于SAH计算,这里将其封装为函数,如下
// in BVH.cpp
double BVHAccel::computeSurfaceArea(std::vector<Object*> objects){
Bounds3 centroidBounds;
for(int i = 0; i < objects.size(); ++i){
centroidBounds = Union(centroidBounds, objects[i]->getBounds().Centroid());
}
return centroidBounds.SurfaceArea();
}记得修改BVHAccel构造函数,加入BVH构建划分方式的判断
// in BVH.cpp
// BVHAccel::BVHAccel(std::vector<Object*> p, int maxPrimsInNode, SplitMethod splitMethod)
if(splitMethod == BVHAccel::SplitMethod::NAIVE)
root = recursiveBuild(primitives);
else
root = recursiveBuildSAH(primitives);在此处修改使用的划分方法
// in BVH.hpp
BVHAccel(std::vector<Object*> p, int maxPrimsInNode = 1, SplitMethod splitMethod = SplitMethod::SAH);效果

时间对比
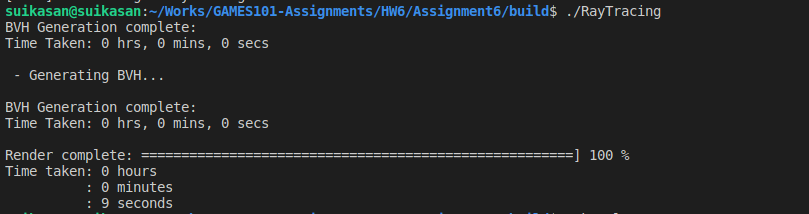
原始方法
SAH方法
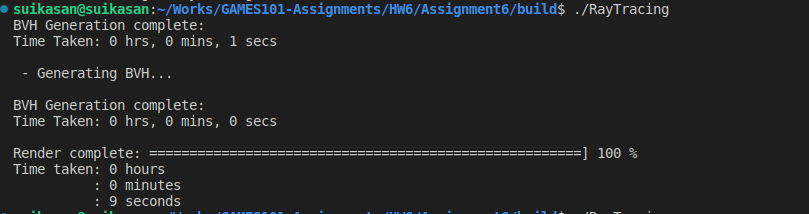
不知道是因为三角面元数量不够多还是什么原因,SAH方法相较于普通中分法构建BVH的提升在本机上面看不出来,我查阅了其他文章发现结果也是大同小异,不太明显。
代码框架说明
本次作业代码框架由作业5更新修改而来,除了新增BVH类、Bounds类以外,其他大同小异。原先的部分函数被拆分到其他类中,比如原先Renderer类中的castRay和fresnel到了Scene类中。
// in document
• Material.hpp: 我们从将材质参数拆分到了一个单独的类中,现在每个物体实
例都可以拥有自己的材质。
• Intersection.hpp: 这个数据结构包含了相交相关的信息。
• Ray.hpp: 光线类,包含一条光的源头、方向、传递时间 t 和范围 range.
• Bounds3.hpp: 包围盒类,每个包围盒可由 pMin 和 pMax 两点描述(请思考
为什么)。Bounds3::Union 函数的作用是将两个包围盒并成更大的包围盒。
与材质一样,场景中的每个物体实例都有自己的包围盒。
• BVH.hpp: BVH 加速类。场景 scene 拥有一个 BVHAccel 实例。从根节点开
始,我们可以递归地从物体列表构造场景的 BVH.Bounds
包围盒类中定义了其各种构造函数,还有与光线的求交的函数,判断点是否在其中的函数,包围盒覆盖、合并函数,求表面积函数等等,总体较简单故不具体展开说明,注意其中函数的重载即可。
BVH
理解BVH类的递归构建过程十分重要,下面进行简要说明。
BVHBuildNode* BVHAccel::recursiveBuild(std::vector<Object*> objects)
{
BVHBuildNode* node = new BVHBuildNode();
// Compute bounds of all primitives in BVH node
Bounds3 bounds;
for (int i = 0; i < objects.size(); ++i)
bounds = Union(bounds, objects[i]->getBounds()); //读取每个三角形的包围盒并逐一合并成大包围盒
// 只有一个物体,则该物体就是叶子节点
if (objects.size() == 1) {
// Create leaf _BVHBuildNode_
node->bounds = objects[0]->getBounds();
node->object = objects[0];
node->left = nullptr;
node->right = nullptr;
return node;
}
// 有两个物体,则这两个物体是根节点的左右叶子节点
else if (objects.size() == 2) {
node->left = recursiveBuild(std::vector{objects[0]});
node->right = recursiveBuild(std::vector{objects[1]});
node->bounds = Union(node->left->bounds, node->right->bounds);
return node;
}
else {
Bounds3 centroidBounds;
// 将每个物体的包围盒的中心作为顶点构建大包围盒
for (int i = 0; i < objects.size(); ++i)
centroidBounds =
Union(centroidBounds, objects[i]->getBounds().Centroid());
int dim = centroidBounds.maxExtent();//判断哪个是最长轴(1-x,2-y,3-z)
// 根据最长轴,将物体按照对应轴坐标从小到大排序
switch (dim) {
case 0:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().x <
f2->getBounds().Centroid().x;
});
break;
case 1:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().y <
f2->getBounds().Centroid().y;
});
break;
case 2:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().z <
f2->getBounds().Centroid().z;
});
break;
}
// 将排序好物体对半分开,分别作为左右子节点,并各自递归构建子节点
auto beginning = objects.begin();
auto middling = objects.begin() + (objects.size() / 2);
auto ending = objects.end();
auto leftshapes = std::vector<Object*>(beginning, middling);
auto rightshapes = std::vector<Object*>(middling, ending);
assert(objects.size() == (leftshapes.size() + rightshapes.size()));
node->left = recursiveBuild(leftshapes);
node->right = recursiveBuild(rightshapes);
node->bounds = Union(node->left->bounds, node->right->bounds);
}
return node;
}递归构建BVH函数中,首先读入物体,并根据每个物体的包围盒逐一合并成大包围盒。
对不同物体数量的构建分为三种情况:
- 当仅有一个物体时,该物体包围盒就是当前节点的包围盒,当前节点是叶子节点,左右子节点指针置空;
- 当有两个物体时,两个物体包围盒分别是当前节点的左右叶子节点;
- 当物体数量更多时,根据物体包围盒中心构建覆盖范围包围盒,判断包围盒的长轴(maxExtent()返回0,1,2分别表示长轴为x轴,y轴,z轴),根据物体对应长轴的坐标从小到大排序,再对半分开,分别作为当前节点的左右子节点,然后对左右子节点分别递归构建,直到子节点物体数量为1或2进入上述两种情况后构建完成。
