前言

GAMES101作业系列为GAMES101作业记录(包含作业1-8)，文章中会解释作业内容并附上代码，同时对代码框架进行简要说明。
已完成的代码可在我的GitHubGAMES101作业代码仓库获取。

GAMES101课程相关基础知识可参看本博客GAMES101知识梳理系列。

作业描述

任务说明

本次作业的任务是实现使用控制点绘制出贝塞尔曲线。
主要工作如下：

  • 完成recursive_bezier函数：输入控制点序列和浮点数t，得到当前t对应的贝塞尔曲线上的点
  • 完成bezier函数：实现Bézier曲线的绘制
  • 提高：实现Bézier曲线的反走样

重点提要

主要是对De Casteljau算法的理解，利用其逐阶插值的特点进行代码实现。

完成作业

本次作业中，我将给定的框架进行了少量修改，直接实现对任意控制点数绘制贝塞尔曲线而不是仅仅四个点。
对框架中给出的naive_bezier函数，并未修改成任意控制点数实现。该函数直接用公式表示贝塞尔曲线上的点，用于验证我们实现的De Casteljau算法的正确性，如要将其也改为实现任意控制点数绘制则需要在其中表示出Bernstein多项式。

更改说明

实现对任意控制点数的绘制，需要对给定的代码框架进行一些修改，说明如下

void mouse_handler(int event, int x, int y, int flags, void *userdata) 
{
    if (event == cv::EVENT_LBUTTONDOWN)
    {
        std::cout << "Left button of the mouse is clicked - position (" << x << ", "
        << y << ")" << '\n';
        control_points.emplace_back(x, y);
    }
}

mouse_handler函数的if语句条件中去掉点序列size的限制。

int main() 
{
    cv::Mat window = cv::Mat(700, 700, CV_8UC3, cv::Scalar(0));
    cv::cvtColor(window, window, cv::COLOR_BGR2RGB);
    cv::namedWindow("Bezier Curve", cv::WINDOW_AUTOSIZE);

    cv::setMouseCallback("Bezier Curve", mouse_handler, nullptr);

    int key = -1;
    while (key != 27) 
    {
        for (auto &point : control_points) 
        {
            cv::circle(window, point, 3, {255, 255, 255}, 3);
        }
        /********************edited*********************/
        if (key == 13)
        {
            // naive_bezier(control_points, window);
            bezier(control_points, window);
            cv::imshow("Bezier Curve", window);
            cv::imwrite("my_bezier_curve.png", window);
            key = cv::waitKey(0);
            return 0;
        }
        /***********************************************/
        cv::imshow("Bezier Curve", window);
        key = cv::waitKey(20);
    }
    return 0;
}

main函数中while循环中贝塞尔曲线的绘制部分代码放入if语句中，条件是(key==13)，即当键入Enter时，再进行曲线的绘制。
如此修改后实现的效果是先用鼠标在窗口中按顺序定义出控制点，键入Enter表示定义控制点完成，然后程序根据已定义的控制点进行绘制。

基础

recursive_bezier函数

cv::Point2f recursive_bezier(const std::vector<cv::Point2f> &control_points, float t) 
{
    // TODO: Implement de Casteljau's algorithm
    std::vector<cv::Point2f> points(control_points);
    std::vector<cv::Point2f> ret;
    for (auto i = points.size(); i > 1; --i)
    {
        for (std::size_t j = 0; j < i - 1; ++j)
        {
            auto point = (1 - t) * points[j] + t * points[j + 1];
            ret.push_back(point);
        }
        if (ret.size() == 1)
            break;
        else
        {
            points = ret;
            ret.clear();
        }
    }
    return cv::Point2f(ret[0]);
}

这里是直接实现了对任意点数插值的de Casteljau算法，如果只是完成四个控制点的绘制可以不用循环。
其中，points保存每一趟循环需要插值的点的序列，ret保存插值结果，一趟插值完毕后ret的结果赋值给point，ret清零，也就是说一趟插值的结果即为下一趟需要插值的点。直到某次插值后ret中仅有一个点，该点就是当前t值对应的贝塞尔曲线上的点。

bezier函数

void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window) 
{
    // TODO: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's 
    // recursive Bezier algorithm.
    for (double t = 0.0; t <= 1.0; t += 0.001)
    {
        auto point = recursive_bezier(control_points, t);
        window.at<cv::Vec3b>(point.y, point.x)[1] = 255;
    }
}

bezier函数就是执行绘制的流程，以0.001为步长绘制t从0到1对应的点形成贝塞尔曲线。

效果

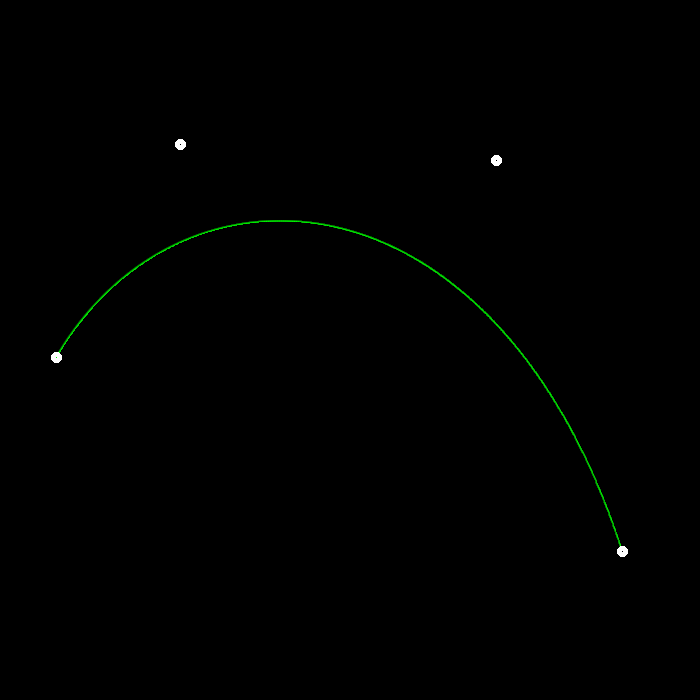
de Casteljau算法绘制结果
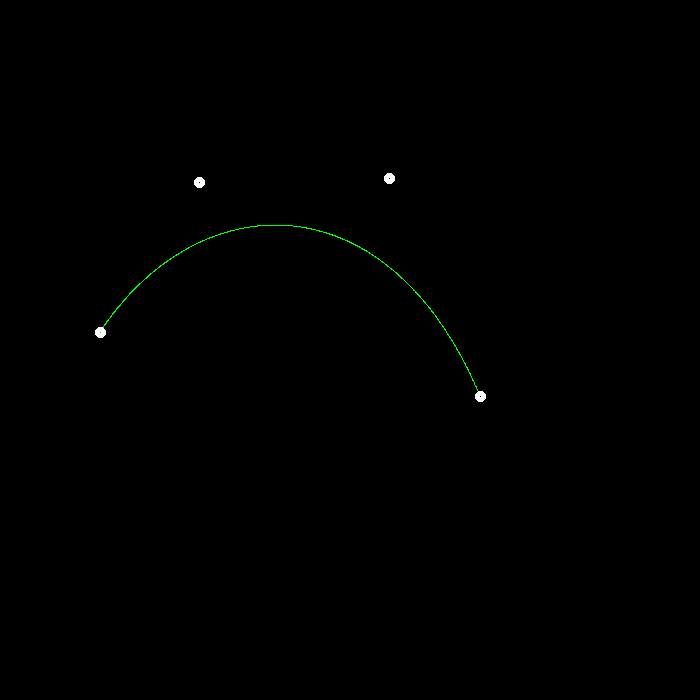
4points

结果验证
同时调用naive_bezier和bezier函数，验证算法正确性
test

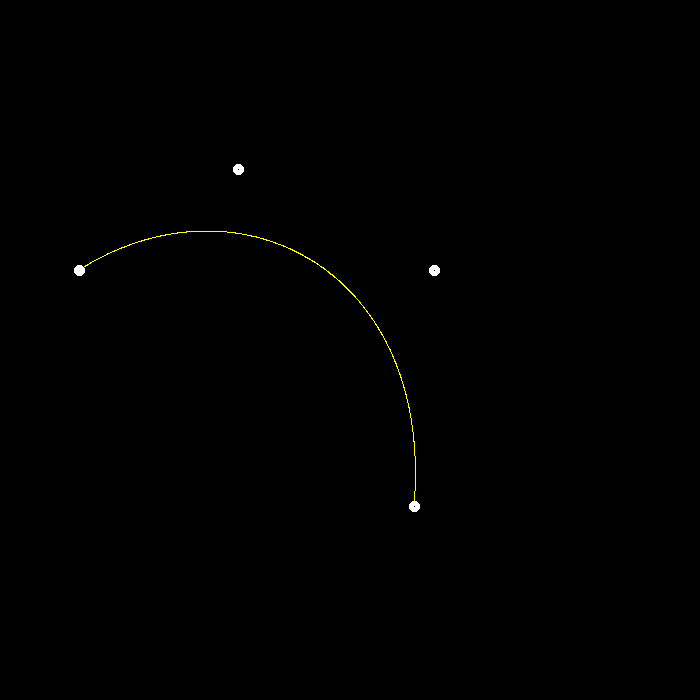
不同数量的控制点
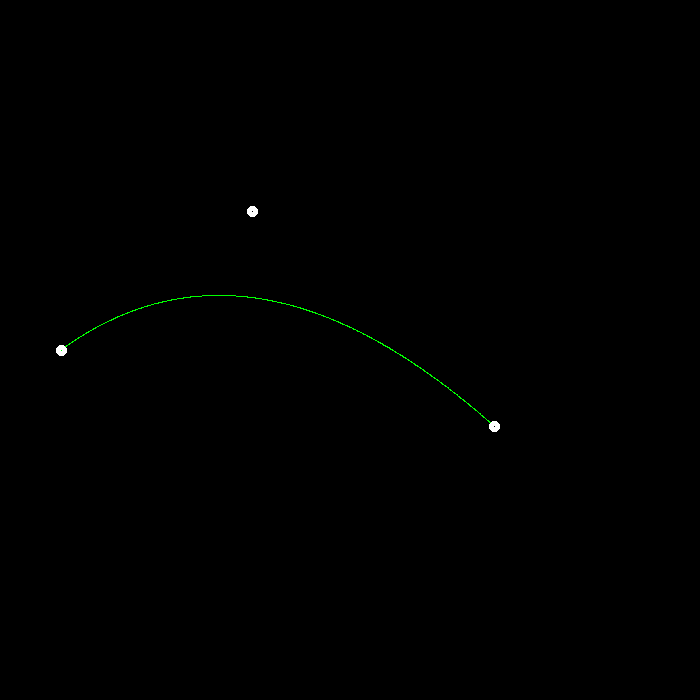
3points
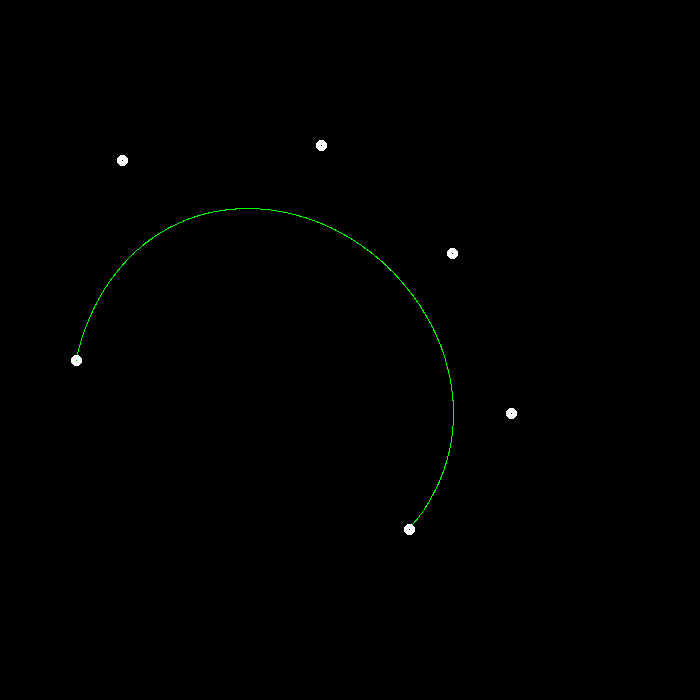
6points

提高

贝塞尔曲线反走样的实现思路参考了csdn大佬ycr的帐号的【GAMES101】作业4（提高）含Bazier曲线的反走样处理文章中的处理思路。

反走样原理解释与实现

这里使用Excel单元格表示像素来解释走样的形成和反走样思路。
我们原来仅绘制计算出的点所在的像素点，像这样
1
根据作业说明文档的提示：对于一个曲线上的点，不只把它对应于一个像素，你需要根据到像素中心的距离来考虑与它相邻的像素的颜色。
因此，我们考虑以当前点所在像素为中心的3×33\times3范围的9个像素，也就是说一个点会影响它附近的9个像素。中心离当前点越近的像素颜色越接近绿色(0,255,0)，中心离当前点越远则越接近背景黑色(0,0,0)。类似这样
2
具体实现就是根据当前点到各像素中心的距离，计算出各像素对应的一个比值，用该比值乘以颜色(0,255,0)为该像素的颜色。其中的距离dd取值范围为[0,3/2][0,3/\sqrt{2}]，因此比值可以表示成

ratio=1−d∗2/3ratio=1-d*\sqrt{2}/3

dd从0变化到1，对应的ratioratio从1线性变化到0，颜色从(0,255,0)线性变化到(0,0,0)，符合上述的思路。

代码如下，我的实现是在bezier函数中加入对相邻像素的操作，前面未涉及的注意点请见代码注释

void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window) 
{
    // TODO: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's 
    // recursive Bezier algorithm.
    for (double t = 0.0; t <= 1.0; t += 0.001)
    {
        auto point = recursive_bezier(control_points, t);
        cv::Point2f pointCenter;//中心的像素
        pointCenter.x = std::floor(point.x + 0.5f);
        pointCenter.y = std::floor(point.y + 0.5f);
        //依次遍历3x3范围内的像素
        for (int i = -1; i < 1; ++i)
        {
            for (int j = -1; j < 1; ++j)
            {
                cv::Point2f pointCurr;
                pointCurr.x = pointCenter.x + i;
                pointCurr.y = pointCenter.y + j;
                //保证像素操作不要超出窗口范围
                if (pointCurr.x > 700 || pointCurr.x < 0 || pointCurr.y>700 || pointCurr.y < 0)
                    continue;
                float distance = sqrt(pow((pointCurr.x - point.x), 2) + pow((pointCurr.y - point.y), 2));
                float ratio = 1 - distance / 3 * sqrt(2);
                int colorG = 255 * ratio;
                //绘制不同点时候会有像素被反复计算，此时保留其颜色的最大值即可
                if (window.at<cv::Vec3b>(pointCurr.y, pointCurr.x)[1] < colorG)
                     window.at<cv::Vec3b>(pointCurr.y, pointCurr.x)[1] = colorG;
            }
        }
    }
}

效果

反走样
antialiasing
前后对比
3
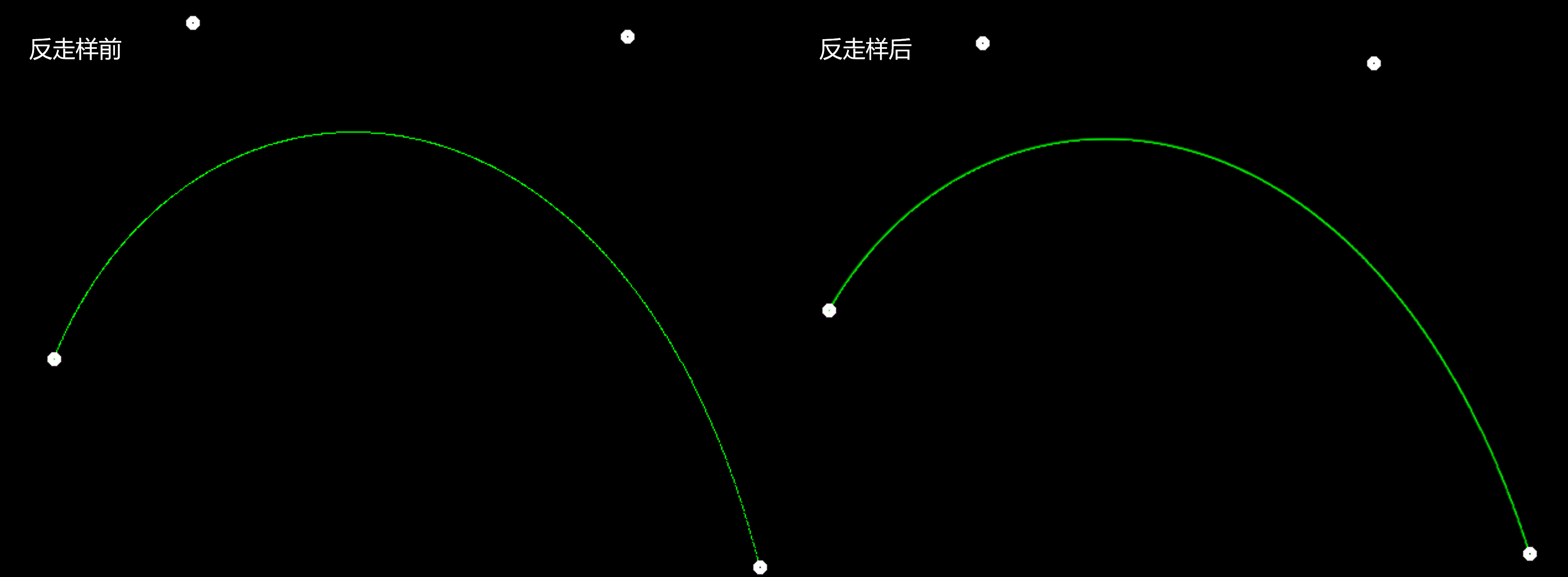
可见，反走样效果还是十分明显的，原先的曲线锯齿严重，且中间有黑点，像断开了似的；反走样后明显改善。